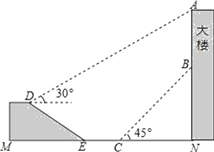
【題目】如圖，鐘鼓樓AN上懸掛一條幅AB，謝高在坡面D處測得條幅頂部A的仰角為30°，沿坡面向下走到坡腳E處，然后向鐘鼓樓方向繼續行走10米來到C處，測得條幅的底部B的仰角為45°，此時謝高距鐘鼓樓底端N處20米．已知坡面DE=20米，山坡的坡度i=1：
（即tan∠DEM=1：），且M、E、C、N在同一條直線上，求條幅的長度（結果精確到1米）
【答案】17米
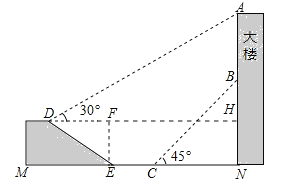
【解析】分析：過點D作DH⊥AN于H，過點E作FE⊥于DH于F，首先求出DF的長，進而可求出DH的長，在直角三角形ADH中，可求出AH的長，進而可求出AN的長，在直角三角形CNB中可求出BN的長，利用AB=AH﹣BN計算即可．
詳解：過點D作DH⊥AN于H，過點E作FE⊥于DH于F．
∵坡面DE=20米，山坡的坡度i=1：
，∴EF=10米，DF=10米．
∵DH=DF+EC+CN=（10+30）米，∠ADH=30°，
∴AH=
×DH=（10+10）米，∴AN=AH+EF=（20+10）米．
∵∠BCN=45°，∴CN=BN=20米，∴AB=AN﹣BN=10≈17米．
答：條幅的長度是17米．
口算題卡加應用題集訓系列答案
綜合自測系列答案科目：初中數學 來源： 題型：
【題目】今年學校舉行足球聯賽，共賽17輪（即每隊均需參賽17場），記分辦法是：勝1場得3分，平1場得1分，負1場得0分．在這次足球比賽中，小虎足球隊得16分，且踢平場數是所負場數的整數倍，則小虎足球隊所負場數的情況有（ ）種
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目：初中數學 來源： 題型：
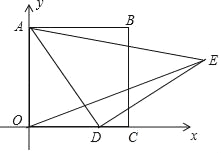
【題目】如圖，在平面直角坐標系中，已知正方形ABCO，A（0，3），點D為x軸上一動點，以AD為邊在AD的右側作等腰Rt△ADE，∠ADE＝90°，連接OE，則OE的最小值為（ ）
A. 
B. 
C. 2D. 3
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有20筐橘子，以每筐20千克為標準，超過或不足的部分分別用正數或負數來表示，記錄如下：
與標準重量的差(單位：千克) | －2 | －1.5 | －1 | 0 | 1 | 1.5 |
筐 數 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)求最重的一筐比最輕的一筐重多少？
(2)求20筐橘子的總重量是多少千克？
查看答案和解析>>
科目：初中數學 來源： 題型：
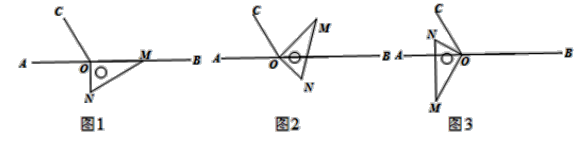
【題目】如圖1，點O為直線AB上一點，過點O作射線OC，使∠BOC=120°，將一直角三角板的直角頂點放在點O處，一邊OM在射線OB上，另一邊ON在直線AB的下方．
（1）如圖2，將圖1中的三角板繞點O逆時針旋轉，使邊OM在∠BOC的內部，且OM恰好平分∠BOC．此時∠AOM=_______度；
（2）如圖3，繼續將圖2中的三角板繞點O按逆時針方向旋轉，使得ON在∠AOC的內部．探究∠AOM與∠NOC之間數量關系，并說明你的理由；
（3）將圖1中的三角板繞點O以每秒10°的速度沿逆時針方向旋轉一周，在旋轉的過程中，若直線ON恰好平分∠AOC，則此時三角板繞點O旋轉的時間是多少秒？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某部隊新兵入伍時，對新兵進行“引體向上”測試，以50次為標準，超過50次用正數表示，不足50次用負數表示，第二小隊的10名新兵的成績如下表：
3 |
| 0 | 8 | 7 |
| 10 | 1 |
| 5 |
（1）求第二小隊的總成績；
（2）求第二小隊的平均成績。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：在數軸上點A表示數a,點B表示數b,點C表示數c,a是多項式2x24x+1的一次項系數,b是最小的正整數,單項式
x2y4的次數為c.
(1)a=___，b=___，c=___；
(2)若將數軸在點B處折疊,則點A與點C___重合(填“能”或“不能”)；
(3)點A,B,C開始在數軸上運動,若點C以每秒1個單位長度的速度向右運動,同時,點A和點B分別以每秒3個單位長度和2個單位長度的速度向左運功,t分鐘過后,若點A與點B之間的距離表示為AB,點B與點C之間的距離表示為BC,則AB=___,BC=___(用含t的代數式表示)；
(4)請問：3ABBC的值是否隨著時間t的變化而改變?若變化，請說明理由；若不變，請求其值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：在平面直角坐標系中，邊長為8的正方形OABC的兩邊在坐標軸上（如圖）．
（1）求點A，B，C的坐標．
（2）經過A，C兩點的直線l上有一點P，點D（0，6）在y軸正半軸上，連PD，PB（如圖1），若PB2﹣PD2＝24，求四邊形PBCD的面積．
（3）若點E（0，1），點N（2，0）（如圖2），經過（2）問中的點P有一條平行于y軸的直線m，在直線m上是否存在一點M，使得△MNE為直角三角形？若存在，求M點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知數軸上兩點
、
，其中A表示的數為-2，表示的數為2，若在數軸上存在一點
，使得
，則稱點叫做點、的“
節點”，例如圖1所示，若點表示的數為0，有
，則稱點為點、的“4節點”.
請根據上述規定回答下列問題：
（1）若點為點、的“節點”，且點在數軸上表示的數為-4，求的值.
（2）若點
是數軸上點、的“5節點”，請你直接寫出點表示的數為____________；
（3）若點
在數軸上（不與、重合），滿足、之間的距離是、之間距離的一半，且此時點為點、的“節點”，求的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
