Question

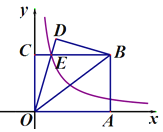
【題目】如圖，在直角坐標系中，矩形OABC的頂點A在x軸上，頂點C在y軸上，B（4，3），連接OB，將△OAB沿直線OB翻折，得△ODB，OD與BC相交于點E，若雙曲線經過點E，則k=_____；

Answer 1

【答案】

【解析】由翻折可知BD=OC, ∠D=∠BCO, 又∵∠CEO=∠DEB,

∴△COE∽△DBE.

∴OE=BE,

設CE=x，則OE=8-x，

在Rt△COE中，根據勾股定理得OC+CE=OE,即3+x=（4-x），解得，

∴k=.

點睛:折疊與翻折類試題主要有四個特點:(1)折疊與翻折類試題常常與線段垂直平分線，等腰三角形，全等三角形，相似三角形，解直角三角形等內容結合在一起；（2）在折疊與翻折的過程中尋找不變量，在折疊與翻折的過程中挖掘新生成的特殊圖形（或常見的基本圖形），立足翻折不變量，考查翻折的新生成；（3）將方程，銳角三角函數，解直角三角形和折疊與翻折融合在一起考查；（4）直角，中點，角平分線，相似三角形，銳角三角函數，解直角三角形，方程思想，轉化與化歸是解決折疊與翻折問題的常見關鍵詞.