
【題目】如圖,矩形ABCD,點E是邊AD上一點,過點E作EF⊥BC,垂足為點F,將△BEF繞著點E逆時針旋轉,使點B落在邊BC上的點N處,點F落在邊DC上的點M處,如果點M恰好是邊DC的中點,那么 ![]() 的值是 .
的值是 . 
【答案】![]()
【解析】解:如圖, 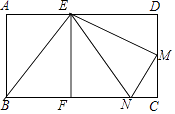
將△BEF繞著點E逆時針旋轉得到△EMN,
∴BE=EN,EM=EF,MN=BF,
∵EF⊥BC,
∴BF=FN,
∴BF=FN=NM,
∵EF⊥BC,
∴四邊形EFCD是矩形,
∴EF=CD,
∵點M恰好是邊DC的中點,
∴DM= ![]() CD=
CD= ![]() EM,
EM,
∴∠DEM=30°,
∴∠DME=60°,
∵∠NME=90°,
∴∠CMN=30°,
設CN=x,
∴MN=2x,CM= ![]() x,
x,
∴CD=2 ![]() x,
x,
∴BF=FN=NM=2x,
∴BC=5x,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考點精析】認真審題,首先需要了解矩形的性質(矩形的四個角都是直角,矩形的對角線相等),還要掌握旋轉的性質(①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了)的相關知識才是答題的關鍵.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在銳角△ABC中,BC=10,高AD=8,矩形EFPQ的一邊QP在BC邊上,E、F兩點分別在AB、AC上,AD交EF于點H.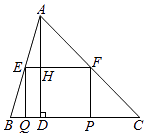
(1)求證: ![]() =
= ![]() ;
;
(2)設EF的長為x.
①當x為何值時,矩形EFPQ為正方形?
②當x為何值時,矩形EFPQ的面積最大?并求其最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y=﹣ ![]() x+3與x軸、y軸分別交于A、B兩點,設O為坐標原點.
x+3與x軸、y軸分別交于A、B兩點,設O為坐標原點.
(1)求∠ABO的正切值;
(2)如果點A向左平移12個單位到點C,直線l過點C且與直線y=﹣ ![]() x+3平行,求直線l的解析式.
x+3平行,求直線l的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在正方形ABCD中,P在對角線AC上,E在AC的延長線上,PB=PM , DE=EF.
(1)求證:∠CDE=∠F;
(2)若AB=5,CM=1,求PB的長;
(3)如圖2,若BF=10,△QCF是以CF為底的等腰三角形,連接DQ , 試求△CDQ的最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,半圓O的直徑AB=10,有一條定長為6的動弦CD在弧AB上滑動(點C、點D分別不與點A、點B重合),點E、F在AB上,EC⊥CD,FD⊥CD. 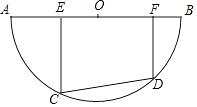
(1)求證:EO=OF;
(2)聯結OC,如果△ECO中有一個內角等于45°,求線段EF的長;
(3)當動弦CD在弧AB上滑動時,設變量CE=x,四邊形CDFE面積為S,周長為l,問:S與l是否分別隨著x的變化而變化?試用所學的函數知識直接寫出它們的函數解析式及函數定義域,以說明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中有△ABC,若小方格邊長為1,請你根據所學的知識解答下列問題:
(1)判斷△ABC是什么形狀?并說明理由.
(2)求△ABC中BC邊上的高.
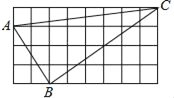
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我省某工藝廠為全運會設計了一款成本為每件20元的工藝品,投放市場試銷后發現每天的銷售量y(件)是售價x(元/件)的一次函數。當售價為22元/件時,每天銷售量為780件;當售價為25元/件時,每天銷售量為750件。
(1)求y與x的函數關系式;
(2)如果該工藝品售價最高不超過每件30元,那么售價定為每件多少元時,工藝廠銷售該工藝品每天獲得的利潤最大?最大利潤是多少元?(利潤=售價-成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,山坡上有一顆樹AB,樹底部B點到山腳C點的距離BC為6 ![]() 米,山坡的坡角為30°,小宇在山腳的平地F處測量這棵樹的高,點C到測角儀EF的水平距離CF=1米,從E處測得樹頂部A的仰角為45°,樹底部B的仰角為20°,求樹AB的高度.
米,山坡的坡角為30°,小宇在山腳的平地F處測量這棵樹的高,點C到測角儀EF的水平距離CF=1米,從E處測得樹頂部A的仰角為45°,樹底部B的仰角為20°,求樹AB的高度.
(參考數值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com