
【題目】(本題滿分![]() 分)
分)
(![]() )【問題】如圖
)【問題】如圖![]() ,點
,點![]() 為線段
為線段![]() 外一動點,且
外一動點,且![]() ,
, ![]() .當點
.當點![]() 位于__________時線段
位于__________時線段![]() 的長取得最大值,且最大值為__________(用含
的長取得最大值,且最大值為__________(用含![]() 、
、![]() 的式子表示).
的式子表示).
(![]() )【應用】點
)【應用】點![]() 為線段
為線段![]() 除外一動點,且
除外一動點,且![]() ,
, ![]() .如圖
.如圖![]() 所示,分別以
所示,分別以![]() 、
、![]() 為邊,
為邊,
作等邊三角形![]() 和等邊三角形
和等邊三角形![]() ,連接
,連接![]() 、
、![]() .
.
①請找出圖中與![]() 相等的線段,并說明理由.
相等的線段,并說明理由.
②直接寫出線段![]() 長的最大值.
長的最大值.
(![]() )【拓展】如圖
)【拓展】如圖![]() ,在平面直角坐標系中,點
,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 為線段
為線段
![]() 外一動點,且
外一動點,且![]() ,
, ![]() ,
, ![]() .請直接寫出線段
.請直接寫出線段![]() 長的最大值及此時點
長的最大值及此時點![]() 的坐標.
的坐標.




【答案】(![]() )
)![]() 延長線上,
延長線上, ![]() ;(
;(![]() )①
)①![]() ;②
;②![]() (
(![]() )
)![]() ;
; ![]()
【解析】(![]() )當三點不共線時,三角形兩邊之和大于第三邊,即
)當三點不共線時,三角形兩邊之和大于第三邊,即![]() ;
;
當![]() 在
在![]() 延長線上時,
延長線上時, ![]() ;
;
當![]() 在線段
在線段![]() 上時,
上時, ![]() .
.
故當![]() 在
在![]() 延長線上時,
延長線上時, ![]() 取得最大值,且為
取得最大值,且為![]() .
.
(![]() )①依題意得
)①依題意得![]() ,
, ![]() ,利用等邊三角形每個角都是
,利用等邊三角形每個角都是![]() 和角的關系得
和角的關系得![]() ,
,
最后根據邊角邊定理證明![]() ≌
≌![]() ,
,
從而推出![]() .
.
②因為![]() ,所以線段
,所以線段![]() 的最大值即
的最大值即![]() 的最大值.
的最大值.
根據三角形兩邊之和大于第三邊,所以![]() 最大時即
最大時即![]() 、
、![]() 、
、![]() 三點共線,
三點共線,
得到![]() 的最大值為
的最大值為![]() ,
,
故![]() 的最大值為
的最大值為![]() .
.
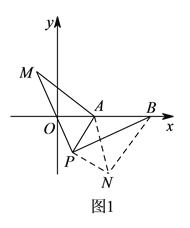
(![]() )如圖1,以點
)如圖1,以點![]() 為圓心,
為圓心, ![]() 為半徑作弧,交以點
為半徑作弧,交以點![]() 為圓心,
為圓心,
![]() 為半徑作的弧于點
為半徑作的弧于點![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,則
,則![]() .
.
在![]() 和
和![]() 中,
中,
 ,
,
所以![]() ≌
≌![]() ,
,
所以![]() ,又因為
,又因為![]() ,
,
所以![]() ,即
,即![]() .
.
由(![]() )可知,當點
)可知,當點![]() 在
在![]() 的延長線上時,
的延長線上時, ![]() 取得最大值,
取得最大值,
又因為![]() ,所以此時
,所以此時![]() 取得最大值.
取得最大值.
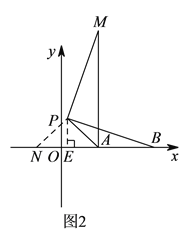
如圖2,點![]() 在
在![]() 的延長線上時,過點
的延長線上時,過點![]() 作
作![]() 軸于點
軸于點![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得
![]() ,
,
所以![]() .
.
因為![]() ,
, ![]() ,所以
,所以![]() 是等腰直角三角形,
是等腰直角三角形,
又因為![]() ,所以
,所以![]() ,
,
又因為點![]() ,
,
所以![]() ,
,
所以點![]() 坐標為
坐標為![]() .
.


科目:初中數學 來源: 題型:
【題目】張老師于2014年2月份在赤峰某縣城買了一套樓房,當時(即2月份)在農行借了9萬元住房貸款,貸款期限為6年,從開始貸款的下一個月起逐月償還,貸款月利率是0.5%,每月還款數額=平均每月應還的貸款本金數額+月利息,月利息=上月所剩貸款本金數額×月利率.
(1)求張老師借款后第一個月應還款的數額;
(2)假設貸款月利率不變,請寫出張老師借款后第n(n是正整數)個月還款數額p與n之間的函數解析式(不必化簡);
(3)在(2)的條件下,求張老師2016年7月份應還款數額.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2+ax+a-2=0
(1)若該方程有一個實數根為1,求a的值及方程的另一實根.
(2)求證:不論a取何實數,該方程都有兩個不相等的實數根.
查看答案和解析>>
科目:初中數學 來源: 題型:
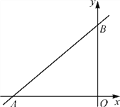
【題目】如圖,直線y=kx+6與x軸,y軸分別相交于點A,B,O為坐標原點,點A的坐標為(-8,0).
(1)求k的值;
(2)若點P(x,y)是第二象限內直線上的一個動點,在點P的運動過程中,試寫出△OPA的面積S與x之間的函數關系式,并寫出自變量的取值范圍;
(3)若點P(0,m)為射線BO(B,O兩點除外)上的一動點,過點P作PC⊥y軸交直線AB于C,連接PA.設△PAC的面積為S′,求S′與m的函數關系式,并寫出自變量m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2013年全國參加高考的人數為9120000人,這個數字用科學記數法表示是( )
A.91.2×105
B.9.12×106
C.9.12×107
D.0.912×107
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com