Question

【題目】已知：關于x的二次函數y=﹣x2+ax（a＞0），點A（n，y1）、B（n+1，y2）、C（n+2，y3）都在這個二次函數的圖象上，其中n為正整數．
（1）y1=y2 ， 請說明a必為奇數；
（2）設a=11，求使y1≤y2≤y3成立的所有n的值；
（3）對于給定的正實數a，是否存在n，使△ABC是以AC為底邊的等腰三角形？如果存在，求n的值（用含a的代數式表示）；如果不存在，請說明理由．

Answer 1

【答案】
（1）

解：∵點A（n，y1）、B（n+1，y2）、C（n+2，y3）都在二次函數y=﹣x2+ax（a＞0）的圖象上，

∴y1=﹣n2+an，y2=﹣（n+1）2+a（n+1）

∵y1=y2，

∴﹣n2+an=﹣（n+1）2+a（n+1）

整理得：a=2n+1

∴a必為奇數

（2）

解：當a=11時，∵y1≤y2≤y3

∴﹣n2+11n≤﹣（n+1）2+11（n+1）≤﹣（n+2）2+11（n+2）

化簡得：0≤10﹣2n≤18﹣4n，

解得：n≤4，

∵n為正整數，

∴n=1、2、3、4

（3）

解：假設存在，則BA=BC，如右圖所示．

過點B作BN⊥x軸于點N，過點A作AD⊥BN于點D，CE⊥BN于點E．

∵xA=n，xB=n+1，xC=n+2，

∴AD=CE=1．

在Rt△ABD與Rt△CBE中，

，

∴Rt△ABD≌Rt△CBE（HL）．

∴∠ABD=∠CBE，即BN為頂角的平分線．

由等腰三角形性質可知，點A、C關于BN對稱，

∴BN為拋物線的對稱軸，點B為拋物線的頂點，

∴n+1= ，

∴n= ﹣1．

∴a為大于2的偶數，存在n，使△ABC是以AC為底邊的等腰三角形，n= ﹣1．

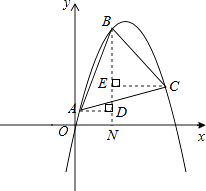
【解析】（1）將點A和點B的坐標代入二次函數的解析式，利用y1=y2得到用n表示a的式子，即可得到答案；（2）將a=11代入解析式后，由題意列出不等式組，求得此不等式組的正整數解；（3）本問為存在型問題．如解答圖所示，可以由三角形全等及等腰三角形的性質，判定點B為拋物線的頂點，點A、C關于對稱軸對稱．于是得到n+1= ，從而可以求出n= ﹣1．
【考點精析】解答此題的關鍵在于理解二次函數的圖象的相關知識，掌握二次函數圖像關鍵點：1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點，以及對二次函數的性質的理解，了解增減性：當a>0時，對稱軸左邊，y隨x增大而減小；對稱軸右邊，y隨x增大而增大；當a<0時，對稱軸左邊，y隨x增大而增大；對稱軸右邊，y隨x增大而減小．