
【題目】如圖,在矩形ABCD中,點O在對角線AC上,以OA的長為半徑的圓O與AD、AC分別交于點E、F,且∠ACB=∠DCE.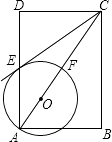
(1)判斷直線CE與⊙O的位置關系,并證明你的結論;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半徑.
,BC=2,求⊙O的半徑.
【答案】
(1)解:直線CE與⊙O相切.
理由如下:
∵四邊形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
連接OE,則∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AE0+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半徑,
∴直線CE與⊙O相切.
(2)解:∵tan∠ACB= ![]() =
= ![]() ,BC=2,
,BC=2,
∴AB=BCtan∠ACB= ![]() ,
,
∴AC= ![]() ;
;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB= ![]() ,
,
∴DE=DCtan∠DCE=1;
方法一:在Rt△CDE中,CE= ![]() =
= ![]() ,
,
連接OE,設⊙O的半徑為r,則在Rt△COE中,CO2=OE2+CE2,即 ![]() =r2+3
=r2+3
解得:r= ![]()
方法二:AE=AD﹣DE=1,過點O作OM⊥AE于點M,則AM= ![]() AE=
AE= ![]()
在Rt△AMO中,OA= ![]() =
= ![]() ÷
÷ ![]() =
= ![]()
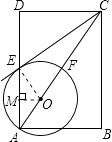
【解析】本題考查了圓的綜合題:圓的切線垂直于過切點的半徑;利用勾股定理計算線段的長.(1)連接OE.欲證直線CE與⊙O相切,只需證明∠CEO=90°,即OE⊥CE即可;(2)在直角三角形ABC中,根據三角函數的定義可以求得AB= ![]() ,然后根據勾股定理求得AC=
,然后根據勾股定理求得AC= ![]() ,同理知DE=1;方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2 , 即
,同理知DE=1;方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2 , 即 ![]() =r2+3,從而易得r的值;方法二、過點O作OM⊥AE于點M,在Rt△AMO中,根據三角函數的定義可以求得r的值.
=r2+3,從而易得r的值;方法二、過點O作OM⊥AE于點M,在Rt△AMO中,根據三角函數的定義可以求得r的值.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:
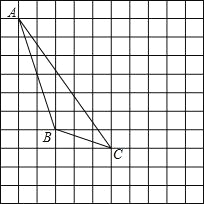
【題目】如圖,每個小正方形的邊長為 1 個單位,每個小方格的頂點叫格點.
(1)畫出△ABC 的 AB 邊上的中線 CD;
(2)畫出△ABC 向右平移 4 個單位后得到的△A1B1C1;
(3)圖中 AC 與 A1C1 的關系是: ;
(4)圖中△ABC 的面積是 ;
(5)能使△BCE 面積為 3 的格點 E 有 個.
查看答案和解析>>
科目:初中數學 來源: 題型:
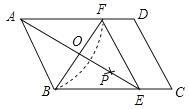
【題目】如圖,在平行四邊形ABCD中,以點A為圓心,AB長為半徑畫弧交AD于點F,再分別以點B、F為圓心,大于![]() BF長為半徑畫弧,兩弧交于一點P,連接AP并延長交BC于點E,連接EF.
BF長為半徑畫弧,兩弧交于一點P,連接AP并延長交BC于點E,連接EF.
(1)四邊形ABEF是 ;(選填矩形、菱形、正方形、無法確定)(直接填寫結果)
(2)AE,BF相交于點O,若四邊形ABEF的周長為40,BF=10,則AE的長為 ,∠ABC= °.(直接填寫結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】情系災區.5月12日我國四川汶川縣發生里氏8.0級大地震,地震給四川,甘肅,陜西等地造成巨大人員傷亡和財產損失.災難發生后,我校師生和全國人民一道,迅速伸出支援的雙手,為災區人民捐款捐物.為了支援災區學校災后重建,我校決定象災區捐助床架60個,課桌凳100套.現計劃租甲、乙兩種貨車共8輛將這些物質運往災區,已知一輛甲貨車可裝床架5個和課桌凳20套,一輛乙貨車可裝床架10個和課桌凳10套.
(1)學校如何安排甲、乙兩種貨車可一次性把這些物資運到災區?有幾種方案?
(2)若甲種貨車每輛要付運輸費1200元,乙種貨車要付運輸費1000元,則學校應選擇哪種方案,使運輸費最少?最少運費是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校校園內有一個大正方形花壇,如圖甲所示,它由四個邊長為3米的小正方形組成,且每個小正方形的種植方案相同.其中的一個小正方形ABCD如圖乙所示,DG=1米,AE=AF=x米,在五邊形EFBCG區域上種植花卉,則大正方形花壇種植花卉的面積y與x的函數圖象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展了“互助、平等、感恩、和諧、進取”主題班會活動,活動后,就活動的5個主題進行了抽樣調查(每位同學只選最關注的一個),根據調查結果繪制了兩幅不完整的統計圖.根據圖中提供的信息,解答下列問題:
(1)這次調查的學生共有多少名?
(2)請將條形統計圖補充完整,并在扇形統計圖中計算出“進取”所對應的圓心角的度數.
(3)如果要在這5個主題中任選兩個進行調查,根據(2)中調查結果,用樹狀圖或列表法,求恰好選到學生關注最多的兩個主題的概率(將互助、平等、感恩、和諧、進取依次記為A、B、C、D、E).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中正確的有( )
①相等的角是對頂角.
②在同一平面內,若a∥b,b∥c,則a∥c.
③若點P(m+3,m+1)在x軸上,則點P的坐標為(4,0).
④數軸上每一個點都表示唯一一個實數.
⑤若a大于0,b不大于0,則點P(-a,-b)在第三象限.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線AC,BD相交于點O,點E,F在BD上,BE=DF.
(1)求證:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com