【題目】如圖，在長度為1個單位長度的小正方形組成的正方形網格中，△ABC的三個頂點A、B、C都在格點上.
（1）在圖1中畫出與△ABC關于直線l成軸對稱的△A1B1C1；
（2）在圖1中直線l上找出一點Q,使得 QA+QC1的值最小；
（3）在圖1中直線l上找出一點P,使得 |PAPC1| 的值最大；
（4）在圖2中，作一個
，E、F都在格點上，使線段BC為△BEF的角平分線
暑假作業海燕出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，A為y軸正半軸上一點，過點A作x軸的平行線，交函數
的圖象于B點，交函數
的圖象于C，過C作y軸和平行線交BO的延長線于D．
（1）如果點A的坐標為（0，2），求線段AB與線段CA的長度之比；
（2）如果點A的坐標為（0，a），求線段AB與線段CA的長度之比；
（3）在（1）條件下，四邊形AODC的面積為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學問題：計算
（其中m，n都是正整數，且m≥2，n≥1）．
探究問題：為解決上面的數學問題，我們運用數形結合的思想方法，通過不斷地分割一個面積為1的正方形，把數量關系和幾何圖形巧妙地結合起來，并采取一般問題特殊化的策略來進行探究．
探究一：計算
．
第1次分割，把正方形的面積二等分，其中陰影部分的面積為
；
第2次分割，把上次分割圖中空白部分的面積繼續二等分，陰影部分的面積之和為+
；
第3次分割，把上次分割圖中空白部分的面積繼續二等分，…；
…
第n次分割，把上次分割圖中空白部分的面積最后二等分，所有陰影部分的面積之和為++
+…+
，最后空白部分的面積是．
根據第n次分割圖可得等式： +++…+=1﹣．
探究二：計算
+
+
+…+
．
第1次分割，把正方形的面積三等分，其中陰影部分的面積為
；
第2次分割，把上次分割圖中空白部分的面積繼續三等分，陰影部分的面積之和為+
；
第3次分割，把上次分割圖中空白部分的面積繼續三等分，…；
…
第n次分割，把上次分割圖中空白部分的面積最后三等分，所有陰影部分的面積之和為++
+…+
，最后空白部分的面積是．
根據第n次分割圖可得等式： +++…+=1﹣，
兩邊同除以2，得+++…+=﹣
．
探究三：計算
+
+
+…+
．
（仿照上述方法，只畫出第n次分割圖，在圖上標注陰影部分面積，并寫出探究過程）
解決問題：計算
+
+
+…+
．
（只需畫出第n次分割圖，在圖上標注陰影部分面積，并完成以下填空）
根據第n次分割圖可得等式：_________，
所以， +++…+=________．
拓廣應用：計算
+
+
+…+
．
查看答案和解析>>
科目：初中數學 來源： 題型：
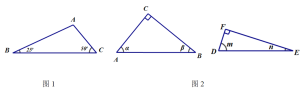
【題目】①如圖1，有一個三角形，它的內角分別為：25°,50°,105°請你把這個三角形分成兩個等腰三角形.畫出你分割的示意圖并標注必要的角度。
②如圖2，有兩個直角三角形，如圖所示，∠C=∠F=90°，∠A, ∠B, ∠D, ∠E的度數分別是
，它們互不相等。請你將這兩個三角形分別分割成兩個三角形，使
所分成的兩個三角形與
所分成的兩個三角形角度對應相等。畫出你分割的示意圖并用字母標注必要的角度。
③如圖3，在正方形
所在平面內找一點
，使其與正方形中的每一邊所構成的三角形均為等腰三角形，這樣的點有________個.
④如圖4，在等邊△ABC所在平面內找一點Q，使其與等邊三角形中的每一邊所構成的三角形均為等腰三角形，這樣的點有________個.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直角坐標系中，在邊長為1的正方形網格中，△AOB的頂點均在格點上，點A，B的坐標分別是A（3，1），B（2，3）．
（1）請在圖中畫出△AOB關于y軸的對稱△A′OB′，點A′的坐標為 ，點B′的坐標為 ；
（2）請寫出A′點關于x軸的對稱點A′'的坐標為 ；
（3）求△A′OB′的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，點A、D在y軸正半軸上，點B、C分別在x軸上，CD平分∠ACB，與y軸交于D點，∠CAO=90°-∠BDO.
（1）求證：AC=BC：
（2）如圖2，點C的坐標為（4，0），點E為AC上一點，且∠DEA=∠DBO，求BC+EC的長；
（3）如圖3，過D作DF⊥AC于F點，點H為FC上一動點，點G為OC上一動點，當H在FC上移動、點G在OC上移動時，始終滿足∠GDH=∠GDO+∠FDH，試判斷FH、GH、OG這三者之間的數量關系，寫出你的結論并加以證明.
（圖3）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】同學們，學習了無理數之后，我們已經把數的領域擴大到了實數的范圍，這說明我們的知識越來越豐富了！可是，無理數究竟是一個什么樣的數呢？下面讓我們在幾個具體的圖形中認識一下無理數.
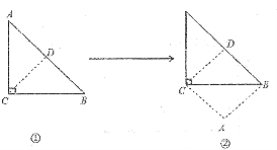
（1）如圖①△ABC是一個邊長為2的等腰直角三角形，它的面積是2，把它沿著斜邊的高線剪開拼成如圖②的正方形ABCD，則這個正方形的面積也就等于正方形的面積即為2，則這個正方形的邊長就是
，它是一個無理數.
（2）如圖，直徑為1個單位長度的圓從原點O沿數軸向右滾動一周，圓上的一點P（滾動時與點O重合）由原點到達點O′，則OO′的長度就等于圓的周長
，所以數軸上點O′代表的實數就是_____，它是一個無理數.
（3）如圖，在Rt△ABC中，∠C=90°，AC=2，BC=1，根據已知可求得AB=_____，它是一個無理數.好了，相信大家對無理數是不是有了更具體的認識了，那么你也試著在圖形中作出兩個無理數吧：
①你能在6×8的網格圖中（每個小正方形邊長均為1），畫出一條長為
的線段嗎？
②學習了實數后，我們知道數軸上的點與實數是一一對應的關系，那么你能在數軸上找到表示－
的點嗎？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
