
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖,給出下列四個結論:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正確結論的是_________(只填序號).

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】對于命題“如果∠1+∠2=90°,那么∠1≠∠2”,能說明它是假命題的反例是( )
A. ∠1=60°,2=40° B. ∠1=50°,∠2=40°
C. ∠1=∠2=40° D. ∠1=∠2=45°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B為定點,定直線l∥AB,P是l上一動點,點M,N分別為PA,PB的中點,對于下列各值:①線段MN的長;②△PAB的周長;③△PMN的面積;④直線MN,AB之間的距離;其中會隨點P的移動而變化的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在¨ABCD中,過點D作DE⊥AB與點E,點F在邊CD上,DF=BE,連接AF,BF

(1)求證:四邊形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求證:AF平分∠DAB.
查看答案和解析>>
科目:初中數學 來源: 題型:
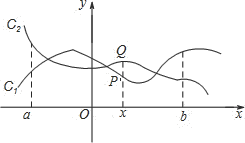
【題目】如圖,點![]() 與
與![]() 分別是兩個函數圖象
分別是兩個函數圖象![]() 與
與![]() 上的任一點.當
上的任一點.當![]() 時,有
時,有![]() 成立,則稱這兩個函數在
成立,則稱這兩個函數在![]() 上是“相鄰函數”,否則稱它們在
上是“相鄰函數”,否則稱它們在![]() 上是“非相鄰函數”.例如,點
上是“非相鄰函數”.例如,點![]() 與
與![]() 分別是兩個函數
分別是兩個函數![]() 與
與![]() 圖象上的任一點,當
圖象上的任一點,當![]() 時,
時, ![]() ,通過構造函數
,通過構造函數![]() 并研究它在
并研究它在![]() 上的性質,得到該函數值得范圍是
上的性質,得到該函數值得范圍是![]() ,所以
,所以![]() 成立,因此這兩個函數在
成立,因此這兩個函數在![]() 上是“相鄰函數”.
上是“相鄰函數”.
(![]() )判斷函數
)判斷函數![]() 與
與![]() 在
在![]() 上是否為“相鄰函數”,并說明理由.
上是否為“相鄰函數”,并說明理由.
(![]() )若函數
)若函數![]() 與
與![]() 在
在![]() 上是“相鄰函數”,求
上是“相鄰函數”,求![]() 的取值范圍.
的取值范圍.
(![]() )若函數
)若函數![]() 與
與![]() 在
在![]() 上是“相鄰函數”,直接寫出
上是“相鄰函數”,直接寫出![]() 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com