
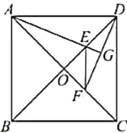
【題目】如圖,已知在正方形![]() 中,對角線
中,對角線![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() ,
,![]() 分別是
分別是![]() 與
與![]() 的平分線,
的平分線,![]() 的延長線與
的延長線與![]() 相交于點
相交于點![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的結論是( )
.其中正確的結論是( )
A.①②B.③④C.①②③D.①②③④
【答案】C
【解析】
由正方形的性質可得∠ACD=∠ADB=45°,根據三角形外角性質及角平分線的定義可得∠AFD=∠ADF,可證明AF=AD,根據等腰三角形“三線合一”的性質可得AG⊥DF,可得AG為DF的垂直平分線,可判定①正確;根據垂直平分線的性質可得EF=ED,可得∠EFD=∠EDF,即可證明∠EFD=∠FDC,可得EF//CD,即可證明EF//AB,可判定②正確;根據正方形的性質可得AB=AD,即可證明AB=AF,可判定③正確,由EF=ED,EF為Rt△EOF的斜邊,可得ED>OE,即可得出EF不是△OCD的中位線,可得CD≠2EF,根據AB=CD即可判定④錯誤;綜上即可得答案.
∵在正方形![]() 中,對角線
中,對角線![]() 與
與![]() 相交于點
相交于點![]() ,
,
∴∠ACD=∠ADB=45°,∠DOC=90°,AB=AD,
∵DF為∠ODC的平分線,
∴∠ODF=∠CDF,
∴∠ADB+∠ODF=∠ACD+∠CDF,即∠AFD=∠ADF,
∴AD=AF,
∵AG為∠OAD的平分線,
∴AG⊥DF,故①正確,
∴AG為DF的垂直平分線,
∴ED=EF,
∴∠EFD=∠EDF,
∴∠EFD=∠CDF,
∴EF//CD,
∵AB//CD,
∴EF//AB,故②正確,
∵AD=AB,AD=AF,
∴AB=AF,故③正確,
∵EF=ED,EF為Rt△EOF的斜邊,
∴ED>OE,
∵EF//CD,
∴EF不是△OCD的中位線,
∴CD≠2EF,即AB≠2EF,故④錯誤,
綜上所述:正確的結論有①②③,
故選:C.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
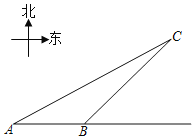
【題目】如圖,我市某景區內有一條自西向東的筆直林蔭路經過景點A、B,現市政決定開發景點C,經考察人員測量,景點A位于景點C的在南偏西60°方向,景點B位于景點C的西南方向,A、B兩景點之間相距380米,現準備由景點C向該林萌路修建一條距離最短的公路,不考慮其它因素,求出這條公路的長?(結果精確到0.1,參考數據:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
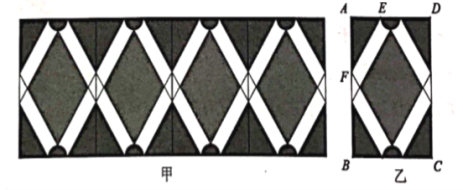
【題目】圖甲是小明設計的花邊圖案作品該作品由形如圖乙的矩形圖案拼接而成(不重疊,無縫隙).該矩形圖案既是軸對稱圖形,又是中心對稱圖形.圖乙中,![]() ,上、下兩個半圓的面積之和為
,上、下兩個半圓的面積之和為![]() ,中間陰影菱形的一組對邊與
,中間陰影菱形的一組對邊與![]() 平行,且菱形的面積比
平行,且菱形的面積比![]() 個角上的陰影三角形的面積之和大
個角上的陰影三角形的面積之和大![]() ,則
,則![]() 的長度為__________
的長度為__________![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為實現2020年全面脫貧的目標,我國實施“精準扶貧”戰略,從而使貧困戶的生活條件得到改善,生活質量明顯提高.為了切實關注、關愛貧困家庭學生,某校對全校各班貧困家庭學生的人數情況進行了統計,統計發現班上貧困家庭學生人數分別有2名,3名,4名,5名,6名,共五種情況.并將其制成了如下兩幅不完整的統計圖:

請回答下列問題:
(1)求該校一共有班級________個;在扇形統計圖中,貧困家庭學生人數有5名的班級所對應扇形圓心角為________°;
(2)將條形圖補充完整;
(3)甲、乙、丙是貧困生中的三名學生,學校決定從這三名學生中隨機抽取兩名代表到市里進行發言,用列表法或畫樹狀圖法,求同時抽到甲,乙兩名學生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
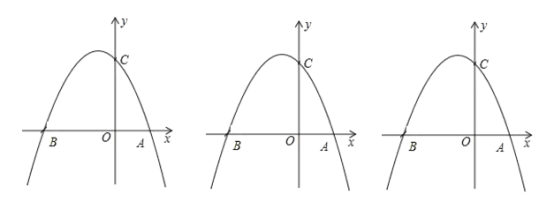
【題目】如圖,在平面直角坐標系中,點![]() 為坐標原點,拋物線
為坐標原點,拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() (
(![]() 左
左![]() 右)兩點,交
右)兩點,交![]() 軸于點
軸于點![]() ,
,![]() ,
,![]() .
.
(1)求拋物線的解析式;
(2)點![]() 為第二象限拋物線上一點,連接
為第二象限拋物線上一點,連接![]() 、
、![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() ,過點
,過點![]() 做
做![]() 軸的垂線,垂足為點
軸的垂線,垂足為點![]() ,過點
,過點![]() 做直線
做直線![]() 軸,在
軸,在![]() 軸上方直線
軸上方直線![]() 上取一點
上取一點![]() ,連接
,連接![]() ,使
,使![]() ,連接
,連接![]() 交
交![]() 軸于點
軸于點![]() ,當
,當![]() 時,求線段
時,求線段![]() 的長;
的長;
(3)在(2)的條件下,點![]() 為第二象限拋物線上的一點,連接
為第二象限拋物線上的一點,連接![]() ,過點
,過點![]() 做
做![]() 于點
于點![]() ,連接
,連接![]() ,線段
,線段![]() 、
、![]() 分別交線段
分別交線段![]() 于點
于點![]() 、
、![]() ,當
,當![]() 時,求
時,求![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
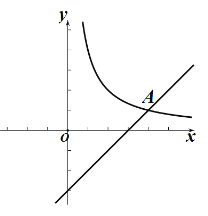
【題目】如圖,在平面直角坐標系xOy中,函數![]() (k>0)的圖象與直線y=x-3相交與點A(4,m).
(k>0)的圖象與直線y=x-3相交與點A(4,m).
(1)求k、m的值;
(2)已知點P(a,a)(a>0),過點P作垂直于y軸的直線,交直線y=x-3于點M,過點P作垂直于x軸的直線,交函數![]() (k>0)的圖象于點N.
(k>0)的圖象于點N.
①當a=1時,判斷PM與PN之間的數量關系,并說明理由;
②若PM≥PN,請結合函數圖象,直接寫出a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .點
.點![]() 為射線
為射線![]() 上一個動點,連接
上一個動點,連接![]() ,點
,點![]() 在直線
在直線![]() 上,且
上,且![]() .過點
.過點![]() 作
作![]() 于點
于點![]() ,點
,點![]() ,
,![]() 在直線
在直線![]() 的同側,且
的同側,且![]() ,連接
,連接![]() .請用等式表示線段
.請用等式表示線段![]() ,
,![]() ,
,![]() 之間的數量關系.小明根據學習函數的經驗.對線段
之間的數量關系.小明根據學習函數的經驗.對線段![]() ,
,![]() ,
,![]() 的長度之間的關系進行了探究.下面是小明的探究過程,請補充完整:
的長度之間的關系進行了探究.下面是小明的探究過程,請補充完整:
(1)對于點![]() 在射線
在射線![]() 上的不同位置,畫圖、測量,得到了線段
上的不同位置,畫圖、測量,得到了線段![]() ,
,![]() ,
,![]() 的長度的幾組值,如下表:
的長度的幾組值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的長度這三個量中,確定 的長度是自變量, 的長度是這個自變量的函數, 的長度是常量.
的長度這三個量中,確定 的長度是自變量, 的長度是這個自變量的函數, 的長度是常量.
(2)在同一平面直角坐標系![]() 中,畫出(1)中所確定的函數的圖象;
中,畫出(1)中所確定的函數的圖象;
(3)結合函數圖象,解決問題:請用等式表示線段![]() ,
,![]() ,
,![]() 之間的數量關系.
之間的數量關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com