
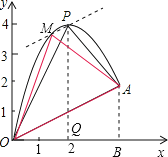
【題目】如圖,一小球從斜坡O點處拋出,球的拋出路線可以用二次函數y=﹣x2+4x刻畫,斜坡可以用一次函數y=![]() x刻畫.
x刻畫.
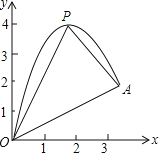
(1)請用配方法求二次函數圖象的最高點P的坐標;
(2)小球的落點是A,求點A的坐標;
(3)連接拋物線的最高點P與點O、A得△POA,求△POA的面積;
(4)在OA上方的拋物線上存在一點M(M與P不重合),△MOA的面積等于△POA的面積.請直接寫出點M的坐標.
【答案】(1)(2,4);(2)(![]() ,
,![]() );(3)
);(3)![]() ;(4)點M的坐標為(
;(4)點M的坐標為(![]() ,
,![]() ).
).
【解析】
試題分析:(1)利用配方法拋物線的一般式化為頂點式,即可求出二次函數圖象的最高點P的坐標;
(2)聯立兩解析式,可求出交點A的坐標;
(3)作PQ⊥x軸于點Q,AB⊥x軸于點B.根據S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入數值計算即可求解;
(4)過P作OA的平行線,交拋物線于點M,連結OM、AM,由于兩平行線之間的距離相等,根據同底等高的兩個三角形面積相等,可得△MOA的面積等于△POA的面積.設直線PM的解析式為y=![]() x+b,將P(2,4)代入,求出直線PM的解析式為y=
x+b,將P(2,4)代入,求出直線PM的解析式為y=![]() x+3.再與拋物線的解析式聯立,得到方程組
x+3.再與拋物線的解析式聯立,得到方程組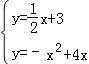 ,解方程組即可求出點M的坐標.
,解方程組即可求出點M的坐標.
解:(1)由題意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函數圖象的最高點P的坐標為(2,4);
(2)聯立兩解析式可得: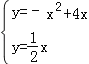 ,
,
解得:![]() ,或
,或![]() .
.
故可得點A的坐標為(![]() ,
,![]() );
);
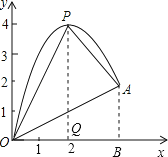
(3)如圖,作PQ⊥x軸于點Q,AB⊥x軸于點B.
S△POA=S△POQ+S△梯形PQBA﹣S△BOA
=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() ﹣2)﹣
﹣2)﹣![]() ×
×![]() ×
×![]()
=4+![]() ﹣
﹣![]()
=![]() ;
;
(4)過P作OA的平行線,交拋物線于點M,連結OM、AM,則△MOA的面積等于△POA的面積.
設直線PM的解析式為y=![]() x+b,
x+b,
∵P的坐標為(2,4),
∴4=![]() ×2+b,解得b=3,
×2+b,解得b=3,
∴直線PM的解析式為y=![]() x+3.
x+3.
由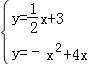 ,解得
,解得![]() ,
,![]() ,
,
∴點M的坐標為(![]() ,
,![]() ).
).


 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:初中數學 來源: 題型:
【題目】在一個不透明的袋子里裝有黃色、白色乒乓球共40個,除顏色外其他完全相同.小明從這個袋子中隨機摸出一球,放回.通過多次摸球實驗后發現,摸到黃色球的概率穩定在15%附近,則袋中黃色球可能有 個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】電腦病毒傳播快,如果一臺電腦被感染,經過兩輪感染后就會有81臺電腦被感染.若每輪感染中平均一臺電腦會感染x臺電腦,則下面所列方程中正確的是( )
A.x(x+1)=81 B.1+x+x2=81
C.(1+x)2=81 D.1+(1+x)2=81
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數的圖象與x軸、y軸分別相交于A、B兩點,且與反比例函數y=![]() (k≠0)的圖象在第一象限交于點C,如果點B的坐標為(0,2),OA=OB,B是線段AC的中點.
(k≠0)的圖象在第一象限交于點C,如果點B的坐標為(0,2),OA=OB,B是線段AC的中點.
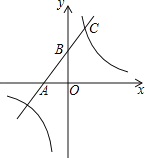
(1)求點A的坐標及一次函數解析式.
(2)求點C的坐標及反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
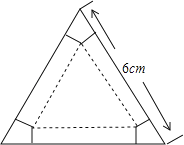
【題目】如圖,有一塊邊長為6cm的正三角形紙板,在它的三個角處分別截去一個彼此全等的箏形,再沿圖中的虛線折起,做成一個無蓋的直三棱柱紙盒,則該紙盒側面積的最大值是( )
A.![]() cm2 B.
cm2 B.![]()
![]() cm2 C.
cm2 C.![]()
![]() cm2 D.
cm2 D.![]()
![]() cm2
cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=BC,BE⊥AC于點E,AD⊥BC于點D,∠BAD=45°,AD與BE交于點F,連接CF.
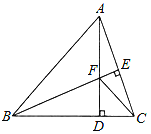
(1)求證:BF=2AE;
(2)若CD=![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+3交x軸于A、B兩點(A在B左邊),交y軸于C點,且OC=3OA,對稱軸x=1交拋物線于D點.
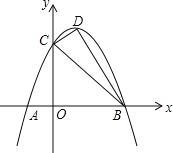
(1)求拋物線解析式;
(2)在直線BC上方的拋物線上找點E使S△BCD=S△BCE,求E點的坐標;
(3)在x軸上方的拋物線上,是否存在點M,過M作MN⊥x軸于N點,使△BMN與△BCD相似?若存在,請求出M的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com