
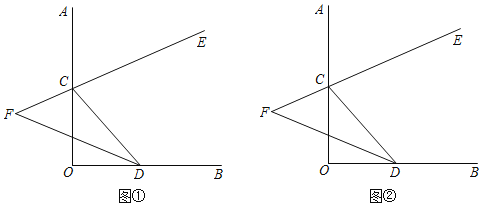
【題目】如圖,∠AOB=90°,點C,D分別在射線OA,OB上,CE是∠ACD的平分線,CE的反向延長線與∠CDO的平分線交于點F.
(1)當∠OCD=56°(如圖①),試求∠F;
(2)當C,D在射線OA、OB上任意移動時(不與點O重合)(如圖②),∠F的大小是否變化?若變化,請說明理由若不變化求出∠F.
【答案】(1)∠F=45°;(2)不變,∠F=45°.
【解析】
(1)首先求出∠CDO=34°,∠ACD=124°,進而得到∠ECD=62°,∠CDF=17°,再根據三角形的外角等于與它不相鄰的兩內角之和,可求∠F=∠ECD﹣∠CDF;
(2)根據三角形外角的性質和角平分線定義求出∠ECD=![]() (90°+∠CDO),∠CDF=
(90°+∠CDO),∠CDF=![]() ∠CDO,然后根據三角形的外角等于與它不相鄰的兩內角之和,可求∠F=∠ECD﹣∠CDF.
∠CDO,然后根據三角形的外角等于與它不相鄰的兩內角之和,可求∠F=∠ECD﹣∠CDF.
(1)∵∠AOB=90°,∠OCD=56°,
∴∠CDO=34°,∠ACD=124°,
∵CE是∠ACD的平分線,DF是∠CDO的平分線,
∴∠ECD=62°,∠CDF=17°,
∵∠ECD=∠F+∠CDF,
∴∠F=∠ECD -∠CDF =45°;
(2)∠F不變,
∵∠ECD=![]() ∠ACD=
∠ACD=![]() (90°+∠CDO),
(90°+∠CDO),
∴∠ECD=45°+![]() ∠CDO,
∠CDO,
∵∠CDF=![]() ∠CDO,
∠CDO,
∴∠F=∠ECD﹣∠CDF,
=45°+![]() ∠CDO﹣
∠CDO﹣![]() ∠CDO,
∠CDO,
=45°.


科目:初中數學 來源: 題型:
【題目】(1)問題發現,
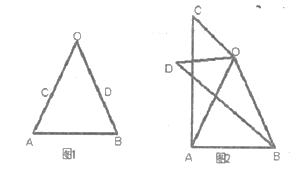
如圖1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一點,將點
上一點,將點![]() 繞點
繞點![]() 順時針旋轉50°得到點
順時針旋轉50°得到點![]() ,則
,則![]() 與
與![]() 的數量關系是________________________。
的數量關系是________________________。
(2)類比探究
如圖2,將(1)中的![]() 繞點
繞點![]() 在平面內旋轉,(1)中的結論是否成立,并就圖2的情形說明理由。
在平面內旋轉,(1)中的結論是否成立,并就圖2的情形說明理由。
(3)拓展延伸
![]() 繞點
繞點![]() 在平面旋轉,當旋轉到
在平面旋轉,當旋轉到![]() 時,請直接寫出
時,請直接寫出![]() 度數。
度數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知命題“等腰三角形兩腰上的高線長相等”
(1)請寫出該命題的逆命題;
(2)判斷(1)中命題的真假,并畫出圖形,補充已知,求證,及證明過程.
圖形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求證:______.
證明:
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點![]() ,以
,以![]() 為直徑在第一象限內作半圓,
為直徑在第一象限內作半圓,![]() 為半圓上一點,連接
為半圓上一點,連接![]() 并延長至
并延長至![]() ,使
,使![]() ,過
,過![]() 作
作![]() 軸于點
軸于點![]() ,交線段
,交線段![]() 于點
于點![]() ,已知
,已知![]() ,拋物線經過
,拋物線經過![]() 、
、![]() 、
、![]() 三點.
三點.

![]() ________°.
________°.
![]() 求拋物線的函數表達式.
求拋物線的函數表達式.
![]() 若
若![]() 為拋物線上位于第一象限內的一個動點,以
為拋物線上位于第一象限內的一個動點,以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形面積記作
為頂點的四邊形面積記作![]() ,則
,則![]() 取何值時,相應的點
取何值時,相應的點![]() 有且只有
有且只有![]() 個?
個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,點F是邊BC的中點,連接AF并延長交DC的延長線于點E,連接AC、BE.
中,點F是邊BC的中點,連接AF并延長交DC的延長線于點E,連接AC、BE.
(1)求證:AB=CE;
(2)若![]() ,則四邊形ABEC是什么特殊四邊形?請說明理由.
,則四邊形ABEC是什么特殊四邊形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“低碳生活,綠色出行”,自行車成為人們喜愛的交通工具.某品牌共享自行車在溫州的投放量自2017年起逐月增加,據統計,該品牌共享自行車1月份投放了640輛,3月份投放了1000輛.
(1)該品牌共享自行車前3個月的投放量的月平均增長率相同,則這三個月一共投放了多少輛自行車?
(2)考慮到增強客戶體驗,該品牌共享自行車準備投入3萬元向自行車生產廠商定制了一批兩種規格比較高檔的自行車,之后投放到某高端寫字樓區域.已知自行車生產廠商生產A型車的成本價為300元/輛,售價為500元/輛,生產B型車的成本價為700元/輛,售價為1000元/輛.根據指定要求,B型車的數量需超過12輛,且A型車的數量不少于B型車的2倍.自行車生產廠商應如何設計生產方案才能獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CD是經過∠BCA的頂點C的一條直線,CA=CB,E,F是直線CD上的兩點,且∠BEC=∠CFA=α.
(1)若直線CD經過∠BCA的內部,且E,F在射線CD上,請解決下面兩個問題:
①如圖(a),若∠BCA=90°,α=90°,則BE________CF,EF________|BE-AF|(填“>”“<”或“=”);
②如圖(b),若0°<∠BCA<180°,請添加一個關于α與∠BCA關系的條件________,使①中的兩個結論仍然成立,并證明兩個結論成立;
(2)如圖(c),若直線CD經過∠BCA的外部,∠BCA=α,請寫出EF,BE,AF三條線段數量關系的合理猜想(不要求證明).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊長為2cm,∠DAB=60°.點P從A點出發,以![]() cm/s的速度,沿AC向C作勻速運動;與此同時,點Q也從A點出發,以1cm/s的速度,沿射線AB作勻速運動.當P運動到C點時,P、Q都停止運動.設點P運動的時間為ts.
cm/s的速度,沿AC向C作勻速運動;與此同時,點Q也從A點出發,以1cm/s的速度,沿射線AB作勻速運動.當P運動到C點時,P、Q都停止運動.設點P運動的時間為ts.
(1)當P異于A.C時,請說明PQ∥BC;
(2)以P為圓心、PQ長為半徑作圓,請問:在整個運動過程中,t為怎樣的值時,⊙P與邊BC分別有1個公共點和2個公共點?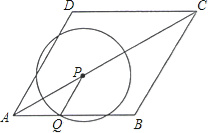
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com