
【題目】如圖,D為直角△ABC的斜邊AB上一點,DE⊥AB交AC于E,如果△AED沿DE翻折,A恰好與B重合,聯結CD交BE于F,如果AC═8,tanA═ ![]() ,那么CF:DF═
,那么CF:DF═ 
【答案】6:5
【解析】解:∵DE⊥AB,tanA═ ![]() , ∴DE=
, ∴DE= ![]() AD,
AD,
∵Rt△ABC中,AC═8,tanA═ ![]() ,
,
∴BC=4,AB= ![]() =4
=4 ![]() ,
,
又∵△AED沿DE翻折,A恰好與B重合,
∴AD=BD=2 ![]() ,DE=
,DE= ![]() ,
,
∴Rt△ADE中,AE= ![]() =5,
=5,
∴CE=8﹣5=3,
∴Rt△BCE中,BE= ![]() =5,
=5,
如圖,過點C作CG⊥BE于G,作DH⊥BE于H,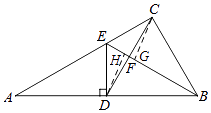
則Rt△BDE中,DH= ![]() =2,
=2,
Rt△BCE中,CG= ![]() =
= ![]() ,
,
∵CG∥DH,
∴△CFG∽△DFH,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
所以答案是:6:5.
【考點精析】根據題目的已知條件,利用翻折變換(折疊問題)和解直角三角形的相關知識可以得到問題的答案,需要掌握折疊是一種對稱變換,它屬于軸對稱,對稱軸是對應點的連線的垂直平分線,折疊前后圖形的形狀和大小不變,位置變化,對應邊和角相等;解直角三角形的依據:①邊的關系a2+b2=c2;②角的關系:A+B=90°;③邊角關系:三角函數的定義.(注意:盡量避免使用中間數據和除法).


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E、F分別是BC、CD上的動點(不與點B,C,D重合),且∠EAF=45°,AE、AF與對角線BD分別相交于點G、H,連接EH、EF,則下列結論:① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE= ![]() AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正確的有( )個。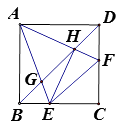
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=2,AC=![]() ,∠BAC=105°,△ABD,△ACE,△BCF都是等邊三角形,則四邊形AEFD的面積為__________.
,∠BAC=105°,△ABD,△ACE,△BCF都是等邊三角形,則四邊形AEFD的面積為__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
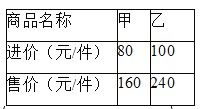
【題目】某商場同時購進甲、乙兩種商品共![]() 件,其進價和售價如右表,設其中甲種商品購進
件,其進價和售價如右表,設其中甲種商品購進![]() 件.
件.
(1)直接寫出購進乙種商品的件數;(用含![]() 的代數式表示)
的代數式表示)
(2)若設該商場售完這![]() 件商品的總利潤為
件商品的總利潤為![]() 元.
元.
①求![]() 與
與![]() 的函數關系式;
的函數關系式;
②該商品計劃最多投入![]() 元用于購買這兩種商品,則至少要購進多少件甲商品?若售完這些商品,則商場可獲得的最大利潤是多少元?
元用于購買這兩種商品,則至少要購進多少件甲商品?若售完這些商品,則商場可獲得的最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形ABCD,P為射線AB上的一點,以BP為邊作正方形BPEF,使點F在線段CB的延長線上,連接EA、EC.
(1)如圖1,若點P在線段AB的延長線上,求證:EA=EC;
(2)若點P在線段AB上.如圖2,連接AC,當P為AB的中點時,判斷△ACE的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強公民的節約意識,我市出臺階梯電價計算方案如下表:
價目表 | |
不超過 |
|
超過 |
|
超過 |
|
注:電費按月結算 | |
![]() 某戶居民
某戶居民![]() 月份應繳電費
月份應繳電費![]() 元,該戶居民
元,該戶居民![]() 月份用電多少度?
月份用電多少度?
![]() 某戶居民
某戶居民![]() 月份用電
月份用電![]() 度,應繳電費
度,應繳電費![]() 元,求
元,求![]() 的值;
的值;
![]() 用
用![]() (度)表示月用電量,請根據
(度)表示月用電量,請根據![]() 的不同取值范圍用含
的不同取值范圍用含![]() 的代數式表示該月應繳電費.
的代數式表示該月應繳電費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的材料
勾股定理神秘而美妙,它的證法多種多樣,下面是教材中介紹的一種拼圖證明勾股定理的方法.

先做四個全等的直角三角形,設它們的兩條直角邊分別為a,b,斜邊為c,然后按圖1的方法將它們擺成正方形.
由圖1可以得到![]() ,
,
整理,得![]() .
.
所以![]() .
.
如果把圖1中的四個全等的直角三角形擺成圖2所示的正方形,
請你參照上述證明勾股定理的方法,完成下面的填空:
由圖2可以得到 ,
整理,得 ,
所以 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出如下結論:①單項式﹣![]() 的系數為﹣
的系數為﹣![]() ,次數為2;②當x=5,y=4時,代數式x2﹣y2的值為1;③化簡(x+
,次數為2;②當x=5,y=4時,代數式x2﹣y2的值為1;③化簡(x+![]() )﹣2(x﹣
)﹣2(x﹣![]() )的結果是﹣x+
)的結果是﹣x+![]() ;④若單項式
;④若單項式![]() ax2yn+1與﹣
ax2yn+1與﹣![]() axmy4的和仍是單項式,則m+n=5.其中正確的結論是_____(填序號)
axmy4的和仍是單項式,則m+n=5.其中正確的結論是_____(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2+(2m﹣1)x+m2=0有兩個實數根x1和x2 .
(1)求實數m的取值范圍;
(2)當x12﹣x22=0時,求m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com