
【題目】(本題滿分10分)
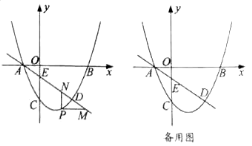
如圖,拋物線![]() 經過點
經過點![]() ,
,![]() ,直線
,直線![]()
![]() 交
交![]() 軸于點
軸于點![]() ,且與拋物線交于
,且與拋物線交于![]() ,
,![]() 兩點.
兩點.![]() 為拋物線上一動點(不與
為拋物線上一動點(不與![]() ,
,![]() 重合).
重合).
(1)求拋物線的解析式;
(2)當點![]() 在直線
在直線![]() 下方時,過點
下方時,過點![]() 作
作![]() 軸交
軸交![]() 于點
于點![]() ,
,![]() 軸交
軸交![]() 于點
于點![]() .求
.求![]() 的最大值;
的最大值;
(3)設![]() 為直線
為直線![]() 上的點,以
上的點,以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形能否構成平行四邊形?若能,求出點
為頂點的四邊形能否構成平行四邊形?若能,求出點![]() 的坐標;若不能,請說明理由.
的坐標;若不能,請說明理由.
【答案】(1)拋物線的解析式為:y=![]() x2-
x2-![]() x-2;(2)
x-2;(2)![]() ;(3)能,(1,0)
;(3)能,(1,0)
【解析】
試題分析:(1)把B(3,0),C(0,-2)代入y=![]() x2+bx+c解方程組即可得到結論;
x2+bx+c解方程組即可得到結論;
(2)設P(m,![]() m2-
m2-![]() m-2),得到N(m,-
m-2),得到N(m,-![]() m-
m-![]() ),M(-m2+2m+2,
),M(-m2+2m+2,![]() m2-
m2-![]() m-2),根據二次函數的性質即可得到結論;
m-2),根據二次函數的性質即可得到結論;
(3)求得E(0,-![]() ),得到CE=
),得到CE=![]() ,設P(m,
,設P(m,![]() m2-
m2-![]() m-2),①以CE為邊,根據CE=PF,列方程得到m=1,m=0(舍去),②以CE為對角線,連接PF交CE于G,CG=GE,PG=FG,得到G(0,-
m-2),①以CE為邊,根據CE=PF,列方程得到m=1,m=0(舍去),②以CE為對角線,連接PF交CE于G,CG=GE,PG=FG,得到G(0,-![]() ),設P(m,
),設P(m,![]() m2-
m2-![]() m-2),則F(-m,
m-2),則F(-m,![]() m-
m-![]() ),列方程得到此方程無實數根,于是得到結論.
),列方程得到此方程無實數根,于是得到結論.
試題解析:(1)把B(3,0),C(0,-2)代入y=![]() x2+bx+c得,
x2+bx+c得,
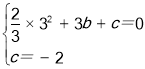
∴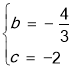
∴拋物線的解析式為:y=![]() x2-
x2-![]() x-2;
x-2;
(2)設P(m,![]() m2-
m2-![]() m-2),
m-2),
∵PM∥x軸,PN∥y軸,M,N在直線AD上,
∴N(m,-![]() m-
m-![]() ),M(-m2+2m+2,
),M(-m2+2m+2,![]() m2-
m2-![]() m-2),
m-2),
∴PM+PN=-m2+2m+2-m-![]() m-
m-![]() -
-![]() m2+
m2+![]() m+2=-
m+2=-![]() m2+
m2+![]() m+
m+![]() =-
=-![]() (m-
(m- ![]() )2+
)2+![]() ,
,
∴當m=![]() 時,PM+PN的最大值是
時,PM+PN的最大值是![]() ;
;
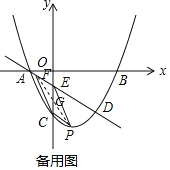
(3)能,
理由:∵y=-![]() x-
x-![]() 交y軸于點E,
交y軸于點E,
∴E(0,-![]() ),
),
∴CE=![]() ,
,
設P(m,![]() m2-
m2-![]() m-2),
m-2),
∵以E,C,P,F為頂點的四邊形能否構成平行四邊形,
①以CE為邊,∴CE∥PF,CE=PF,
∴F(m,-![]() m-
m-![]() ),
),
∴-![]() m-
m-![]() -
-![]() m2+
m2+![]() m+2=
m+2=![]() ,
,
∴m=1,m=0(舍去),
②以CE為對角線,連接PF交CE于G,
∴CG=GE,PG=FG,
∴G(0,-![]() ),
),
設P(m,![]() m2-
m2-![]() m-2),則F(-m,
m-2),則F(-m,![]() m-
m-![]() ),
),
∴![]() ×(
×(![]() m2-
m2-![]() m-2+
m-2+![]() m-
m-![]() )=-
)=-![]() ,
,
∵△<0,
∴此方程無實數根,
綜上所述,當m=1時,以E,C,P,F為頂點的四邊形能否構成平行四邊形.


科目:初中數學 來源: 題型:
【題目】綜合題
(1)發現
如圖,點 ![]() 為線段
為線段 ![]() 外一動點,且
外一動點,且 ![]() ,
, ![]() .
.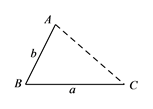
填空:當點 ![]() 位于時,線段
位于時,線段 ![]() 的長取得最大值,且最大值為.(用含
的長取得最大值,且最大值為.(用含 ![]() ,
, ![]() 的式子表示)
的式子表示)
(2)應用
點 ![]() 為線段
為線段 ![]() 外一動點,且
外一動點,且 ![]() ,
, ![]() .如圖所示,分別以
.如圖所示,分別以 ![]() ,
, ![]() 為邊,作等邊三角形
為邊,作等邊三角形 ![]() 和等邊三角形
和等邊三角形 ![]() ,連接
,連接 ![]() ,
, ![]() .
.
①找出圖中與 ![]() 相等的線段,并說明理由;
相等的線段,并說明理由;
②直接寫出線段 ![]() 長的最大值.
長的最大值.
(3)拓展
如圖,在平面直角坐標系中,點 ![]() 的坐標為
的坐標為 ![]() ,點
,點 ![]() 的坐標為
的坐標為 ![]()
![]() 為線段
為線段 ![]() 外一動點,且
外一動點,且 ![]() ,
, ![]() ,
, ![]() ,求線段
,求線段 ![]() 長的最大值及此時點
長的最大值及此時點 ![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用“☆”定義一種新運算:對于任意有理數a和b,規定a☆b=ab2﹣2ab+b.如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27.依據此定義化簡(1﹣3x)☆(﹣4)=____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com