
【題目】如圖,C為線段BD上一動點,分別過點B、D作AB⊥BD,ED⊥BD,連接AC、EC.已知AB=2,DE=1,BD=8,設CD=x.
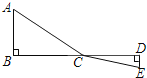
(1)用含x的代數式表示AC+CE的長;
(2)請問點C滿足什么條件時,AC+CE的值最小;
(3)根據(2)中的規律和結論,請構圖求出代數式![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)A、C、E三點共線;(3)13.
;(2)A、C、E三點共線;(3)13.
【解析】
(1)由于△ABC和△CDE都是直角三角形,故AC,CE可由勾股定理求得;
(2)若點C不在AE的連線上,根據三角形中任意兩邊之和>第三邊知,AC+CE>AE,故當A、C、E三點共線時,AC+CE的值最小;
(3)由(1)(2)的結果可作BD=12,過點B作AB⊥BD,過點D作ED⊥BD,使AB=2,ED=3,連接AE交BD于點C,則AE的長即為代數式![]() 的最小值,然后構造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性質可求得AE的值.
的最小值,然后構造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性質可求得AE的值.
解:(1)設CD=x,則BC=8-x,
∵AC=![]() ,CE=
,CE=![]() ,
,
∴AC+CE=![]() +
+![]() ;
;
(2)由兩點之間線段最短可知,當A、C、E三點共線時,AC+CE的值最小;
(3)如右圖所示

作BD=12,過點B作AB⊥BD,過點D作ED⊥BD,使AB=2,ED=3,連接AE交BD于點C,設BC=x,則AE的長即為代數![]() 的最小值.
的最小值.
過點A作AF∥BD交ED的延長線于點F,得矩形ABDF,
則AB=DF=2,AF=BD=12,EF=ED+DF=3+2=5,
所以AE=![]() =
=![]() =13,
=13,
即![]() 的最小值為13.
的最小值為13.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】根據下列條件不能判斷△ABC是直角三角形的是( )
A.∠B=50° ,∠C=40°
B.∠B=∠C=45°
C.∠A,∠B,∠C的度數比為5:3:2
D.∠A-∠B=90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個三角形兩邊中點的連線叫做這個三角形的中位線.只要順次連結三角形三條中位線,則可將原三角形分割為四個全等的小三角形(如圖(1));把三條邊分成三等份,再按照圖(2)將分點連起來,可以看作將整個三角形分成9個全等的小三角形;把三條邊分成四等份,…,按照這種方式分下去,第n個圖形中應該得到( )個全等的小三角形.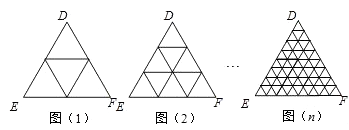
A.![]()
B.![]()
C.![]()
D.(n+1)2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新春佳節來臨,某公司組織10輛汽車裝運蘋果、蘆柑、香梨三種水果共60噸去外地銷售,要求10輛汽車全部裝滿,每輛汽車只能裝運同一種水果,且裝運每種水果的車輛都不少于2輛,根據下表提供的信息,解答以下問題:
蘋果 | 蘆柑 | 香梨 | |
每輛汽車載貨量 | 7 | 6 | 5 |
每車水果獲利 | 2500 | 3000 | 2000 |
![]() 設裝運蘋果的車輛為x輛,裝運蘆柑的車輛為y輛,求y與x之間的函數關系式,并直接寫出x的取值范圍
設裝運蘋果的車輛為x輛,裝運蘆柑的車輛為y輛,求y與x之間的函數關系式,并直接寫出x的取值范圍
![]() 用w來表示銷售獲得的利潤,那么怎樣安排車輛能使此次銷售獲利最大?并求出w的最大值.
用w來表示銷售獲得的利潤,那么怎樣安排車輛能使此次銷售獲利最大?并求出w的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一條高線.若E,F分別是CD和BC上的動點,則BE+EF的最小值是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】港珠澳大橋是世界最長的跨海大橋,連接香港大嶼山、澳門半島和廣東省珠海市,其中珠海站到香港站全長約55千米,2018年10月24日上午9時正式通車.一輛觀光巴士自珠海站出發,25分鐘后,一輛小汽車從同一地點出發,結果同時到達香港站.已知小汽車的速度是觀光巴士的1.6倍,求觀光巴士的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于結論:當a+b=0時,a3+b3=0也成立.若將a看成a3的立方根,b看成b3的立方根,由此得出這樣的結論:“如果兩數的立方根互為相反數,那么這兩個數也互為相反數”
(1)舉一個具體的例子來判斷上述結論是否成立;
(2)若![]() 和
和![]() 互為相反數,且x+5的平方根是它本身,求x+y的立方根.
互為相反數,且x+5的平方根是它本身,求x+y的立方根.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com