
【題目】已知,關(guān)于![]() 的分式方程
的分式方程![]() .
.
(1)當(dāng)![]() ,
,![]() 時(shí),求分式方程的解;
時(shí),求分式方程的解;
(2)當(dāng)![]() 時(shí),求
時(shí),求![]() 為何值時(shí)分式方程
為何值時(shí)分式方程![]() 無(wú)解:
無(wú)解:
(3)若![]() ,且
,且![]() 、
、![]() 為正整數(shù),當(dāng)分式方程
為正整數(shù),當(dāng)分式方程![]() 的解為整數(shù)時(shí),求
的解為整數(shù)時(shí),求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)將a,b的值代入方程得![]() ,解出這個(gè)方程,最后進(jìn)行檢驗(yàn)即可;
,解出這個(gè)方程,最后進(jìn)行檢驗(yàn)即可;
(2)把![]() 代入方程得
代入方程得![]() ,分式方程去分母轉(zhuǎn)化為整式方程為
,分式方程去分母轉(zhuǎn)化為整式方程為![]() ,由分式方程有增根,得11-2b=0,或
,由分式方程有增根,得11-2b=0,或![]() (不存在),或
(不存在),或![]() 求出b的值即可;
求出b的值即可;
(3)把![]() 代入原方程得
代入原方程得![]() ,將分式方程化為整式方程求出x的表達(dá)式,再根據(jù)x是正整數(shù)求出b,然后進(jìn)行檢驗(yàn)即可.
,將分式方程化為整式方程求出x的表達(dá)式,再根據(jù)x是正整數(shù)求出b,然后進(jìn)行檢驗(yàn)即可.
(1)當(dāng)![]() ,
,![]() 時(shí),分式方程為:
時(shí),分式方程為:![]()
解得:![]()
經(jīng)檢驗(yàn):![]() 時(shí)是原方程的解
時(shí)是原方程的解
(2)解:當(dāng)![]() 時(shí),分式方程為:
時(shí),分式方程為:![]()
![]()
①若![]() ,即
,即![]() 時(shí),有:
時(shí),有:![]() ,此方程無(wú)解
,此方程無(wú)解
②若![]() ,即
,即![]() 時(shí),則
時(shí),則
若![]() ,即
,即![]() ,
,![]() ,不成立
,不成立
若![]() ,即
,即![]() ,解得
,解得![]()
∴綜上所述,![]() 或
或![]() 時(shí),原方程無(wú)解
時(shí),原方程無(wú)解
(3)解:當(dāng)![]() 時(shí),分式方程為:
時(shí),分式方程為:![]()
即![]()
∵![]() 是正整數(shù)
是正整數(shù)
∴![]()
∴![]()
即![]()
又∵![]() 是正整數(shù),
是正整數(shù),![]() 是整數(shù).
是整數(shù).
∴![]()
經(jīng)檢驗(yàn),當(dāng)![]() 時(shí),
時(shí),![]() (不符合題意,舍去)
(不符合題意,舍去)
∴![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,在半徑為4的⊙O中,圓心角∠AOB=90°,以半徑OA、OB的中點(diǎn)C、F為頂點(diǎn)作矩形CDEF,頂點(diǎn)D、E在⊙O的劣弧![]() 上,OM⊥DE于點(diǎn)M.試求圖中陰影部分的面積.(結(jié)果保留π)
上,OM⊥DE于點(diǎn)M.試求圖中陰影部分的面積.(結(jié)果保留π)

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,過(guò)點(diǎn)![]() 的直線
的直線![]() 與直線
與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() .
.
(1)直線![]() 的關(guān)系式為 ;直線
的關(guān)系式為 ;直線![]() 的關(guān)系式為 (直接寫(xiě)出答案,不必寫(xiě)過(guò)程).
的關(guān)系式為 (直接寫(xiě)出答案,不必寫(xiě)過(guò)程).
(2)求![]() 的面積.
的面積.
(3)若有一動(dòng)點(diǎn)![]() 沿路線
沿路線![]() 運(yùn)動(dòng),當(dāng)
運(yùn)動(dòng),當(dāng)![]() 時(shí),求點(diǎn)
時(shí),求點(diǎn)![]() 坐標(biāo).
坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
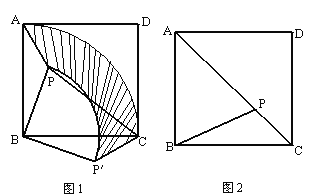
【題目】已知,點(diǎn)P是正方形ABCD內(nèi)的一點(diǎn),連PA、PB、PC.
(1)將△PAB繞點(diǎn)B順時(shí)針旋轉(zhuǎn)90°到△P′CB的位置(如圖1).
①設(shè)AB的長(zhǎng)為a,PB的長(zhǎng)為b(b<a),求△PAB旋轉(zhuǎn)到△P′CB的過(guò)程中邊PA所掃過(guò)區(qū)域(圖1中陰影部分)的面積;
②若PA=2,PB=4,∠APB=135°,求PC的長(zhǎng).
(2)如圖2,若PA2+PC2=2PB2,請(qǐng)說(shuō)明點(diǎn)P必在對(duì)角線AC上.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】我市某中學(xué)有一塊四邊形的空地ABCD,如圖所示,為了綠化環(huán)境,學(xué)校計(jì)劃在空地上種植草皮,經(jīng)測(cè)量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面積.
(2)若每種植1平方米草皮需要200元,問(wèn)總共需投入多少元?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:在平面直角坐標(biāo)系中,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() .
.
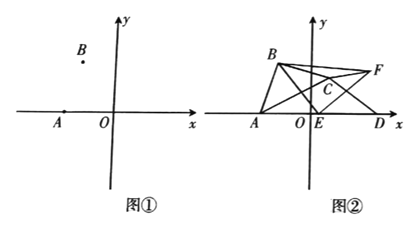
(1)在圖①中的![]() 軸上求作點(diǎn)
軸上求作點(diǎn)![]() ,使得
,使得![]() 的值最小;
的值最小;
(2)若![]() 是以
是以![]() 為腰的等腰直角三角形,請(qǐng)直接寫(xiě)出點(diǎn)
為腰的等腰直角三角形,請(qǐng)直接寫(xiě)出點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)如圖②,在![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() (不與點(diǎn)
(不與點(diǎn)![]() 重合)是
重合)是![]() 軸上一個(gè)動(dòng)點(diǎn),點(diǎn)
軸上一個(gè)動(dòng)點(diǎn),點(diǎn)![]() 是
是![]() 中點(diǎn),連結(jié)
中點(diǎn),連結(jié)![]() ,把
,把![]() 繞著點(diǎn)
繞著點(diǎn)![]() 順時(shí)針旋轉(zhuǎn)
順時(shí)針旋轉(zhuǎn)![]() 得到
得到![]() (即
(即![]() ,
,![]() ),連結(jié)
),連結(jié)![]() 、
、![]() 、
、![]() ,試猜想
,試猜想![]() 的度數(shù),并給出證明.
的度數(shù),并給出證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】平面直角坐標(biāo)系xOy中,橫坐標(biāo)為a的點(diǎn)A在反比例函數(shù)y1═![]() (x>0)的圖象上,點(diǎn)A′與點(diǎn)A關(guān)于點(diǎn)O對(duì)稱,一次函數(shù)y2=mx+n的圖象經(jīng)過(guò)點(diǎn)A′.
(x>0)的圖象上,點(diǎn)A′與點(diǎn)A關(guān)于點(diǎn)O對(duì)稱,一次函數(shù)y2=mx+n的圖象經(jīng)過(guò)點(diǎn)A′.
(1)設(shè)a=2,點(diǎn)B(4,2)在函數(shù)y1、y2的圖象上.
①分別求函數(shù)y1、y2的表達(dá)式;
②直接寫(xiě)出使y1>y2>0成立的x的范圍;
(2)如圖①,設(shè)函數(shù)y1、y2的圖象相交于點(diǎn)B,點(diǎn)B的橫坐標(biāo)為3a,△AA'B的面積為16,求k的值;
(3)設(shè)m=![]() ,如圖②,過(guò)點(diǎn)A作AD⊥x軸,與函數(shù)y2的圖象相交于點(diǎn)D,以AD為一邊向右側(cè)作正方形ADEF,試說(shuō)明函數(shù)y2的圖象與線段EF的交點(diǎn)P一定在函數(shù)y1的圖象上.
,如圖②,過(guò)點(diǎn)A作AD⊥x軸,與函數(shù)y2的圖象相交于點(diǎn)D,以AD為一邊向右側(cè)作正方形ADEF,試說(shuō)明函數(shù)y2的圖象與線段EF的交點(diǎn)P一定在函數(shù)y1的圖象上.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖(1)的長(zhǎng)方形ABCD中,E點(diǎn)在AD上,且BE=2AE.今分別以BE、CE為折線,將A、D向BC的方向折過(guò)去,圖(2)為對(duì)折后A、B、C、D、E五點(diǎn)均在同一平面上的位置圖.若圖(2)中,∠AED=15°,則∠BCE的度數(shù)為_____.
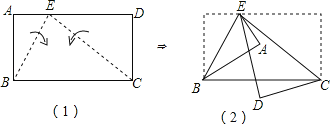
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
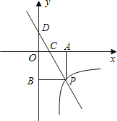
【題目】如圖,一次函數(shù)![]() 的圖象分別交
的圖象分別交![]() 軸、
軸、![]() 軸于點(diǎn)
軸于點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() ,與反比例函數(shù)
,與反比例函數(shù)![]() 的圖象在第四象限的相交于點(diǎn)
的圖象在第四象限的相交于點(diǎn)![]() ,并且
,并且![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,
,![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,已知
,已知![]() ,且
,且![]()
![]() 求上述一次函數(shù)與反比例函數(shù)的表達(dá)式;
求上述一次函數(shù)與反比例函數(shù)的表達(dá)式;
![]() 求一次函數(shù)與反比例函數(shù)的另一個(gè)交點(diǎn)坐標(biāo).
求一次函數(shù)與反比例函數(shù)的另一個(gè)交點(diǎn)坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com