
【題目】如圖(1)所示,∠AOB、∠COD都是直角.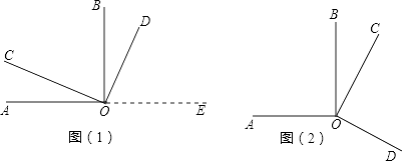
(1)試猜想∠AOD與∠COB在數量上是相等,互余,還是互補的關系.請你用推理的方法說明你的猜想是合理的.
(2)當∠COD繞著點O旋轉到圖(2)所示位置時,你在(1)中的猜想還成立嗎?請你證明你的結論.
【答案】
(1)解:∠AOD與∠COB互補.
理由如下:∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°,
∴∠BOD=∠AOD﹣∠AOB=∠AOD﹣90°,
∠BOD=∠COD﹣∠COB=90°﹣∠COB,
∴∠AOD﹣90°=90°﹣∠COB,
∴∠AOD+∠COB=180°,
∴∠AOD與∠COB互補
(2)解:成立.
理由如下:∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°,
∵∠AOB+∠BOC+∠COD+∠AOD=360°,
∴∠AOD+∠COB=180°,
∴∠AOD與∠COB互補
【解析】(1)∠AOD與∠COB互補.理由如下:根據直角的定義得出∠AOB=∠COD=90°,根據等式的性質得出∠BOD=∠AOD﹣∠AOB=∠AOD﹣90°,∠BOD=∠COD﹣∠COB=90°﹣∠COB,從而得出∠AOD﹣90°=90°﹣∠COB,進而得出∠AOD+∠COB=180°,故得出結論∠AOD與∠COB互補;
(2)當∠COD繞著點O旋轉到圖(2)所示位置時,你在(1)中的猜想還成立:根據垂直的定義及周角的定義得出∠AOB=∠COD=90°,∠AOB+∠BOC+∠COD+∠AOD=360°,從而得出∠AOD+∠COB=180°,得出結論∠AOD與∠COB互補。


科目:初中數學 來源: 題型:
【題目】如圖,BD為□ABCD的對角線,按要求完成下列各題.

(1)用直尺和圓規作出對角線BD的垂直平分線交AD于點E,交BC于點F,垂足為O.(保留作圖痕跡,不要求寫作法)
(2)在(1)的基礎上,連接BE和DF.求證:四邊形BFDE是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.點D在AB邊上,點E是BC邊上一點(不與點B、C重合),且DA=DE,則AD的取值范圍是 . 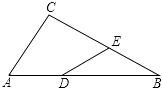
查看答案和解析>>
科目:初中數學 來源: 題型:
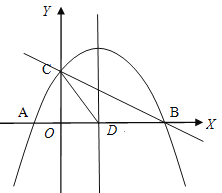
【題目】如圖,拋物線![]() 與x軸交于A(-1,0)、B兩點, 與y軸交于點C(0,2), 拋物線的對稱軸交x軸于點D.
與x軸交于A(-1,0)、B兩點, 與y軸交于點C(0,2), 拋物線的對稱軸交x軸于點D.
(1)求拋物線的解析式;
(2)求sin∠ABC的值;
(3)在拋物線的對稱軸上是否存在點P,使△PCD是以CD為腰的等腰三角形,如果存在,直接寫出點P的坐標;如果不存在,請說明理由;
(4)點E是線段BC上的一個動點,過點E作x軸的垂線與拋物線相交于點F,當點E運動到什么位置時線段EF最長?求出此時E點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,天平呈平衡狀態,其中左側秤盤中有一袋玻璃球,右側秤盤中也有一袋玻璃球,還有2個各20克的砝碼.現將左側袋中一顆玻璃球移至右側秤盤,并拿走右側秤盤的1個砝碼后,天平仍呈平衡狀態,如圖2,則被移動的玻璃球的質量為( )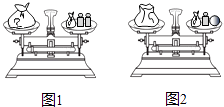
A.10克
B.15克
C.20克
D.25克
查看答案和解析>>
科目:初中數學 來源: 題型:
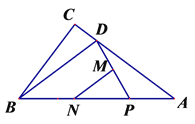
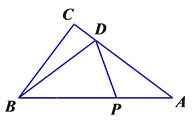
【題目】如圖,在Rt△ABC中,∠C=90°AB=8cm,cos∠ABC=![]() ,點D在邊AC上,且CD=
,點D在邊AC上,且CD=![]() cm,動點P從點A開始沿邊AB向點B以1cm/s的速度移動,當點P到達B點即停止運動.設運動時間為t(s).解答下列問題:
cm,動點P從點A開始沿邊AB向點B以1cm/s的速度移動,當點P到達B點即停止運動.設運動時間為t(s).解答下列問題:
(1)M、N分別是DP、BP的中點,連接MN.
①分別求BC、MN的值;
②求在點P從點A勻速運動到點B的過程中線段MN所掃過區域的面積;
(2)在點P運動過程中,是否存在某一時刻t,使BD平分∠CDP?若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com