
【題目】某市少年宮為小學生開設了繪畫、音樂、舞蹈和跆拳道四類興趣班,為了解學生對這四類興趣班的喜愛情況,對學生進行了隨機問卷調查(問卷調查表如圖所示),將調查結果整理后繪制了一幅不完整的統計表
興趣班 | 頻數 | 頻率 |
A | 0.35 | |
B | 18 | 0.30 |
C | 15 |
|
D | 6 | |
合計 |
| 1 |
請你根據統計表中提供的信息回答下列問題:
(1)統計表中的![]() ,
,![]() ;
;
(2)根據調查結果,請你估計該市2000名小學生中最喜歡“繪畫”興趣的人數;
(3)王姝和李要選擇參加興趣班,若他們每人從![]() 、
、![]() 、
、![]() 、
、![]() 四類興趣班中隨機選取一類,請用畫樹狀圖或列表格的方法,求兩人恰好選中同一類的概率.
四類興趣班中隨機選取一類,請用畫樹狀圖或列表格的方法,求兩人恰好選中同一類的概率.
【答案】(1)![]() ,
,![]() ;(2)最喜歡繪畫興趣的人數為700人;(3)
;(2)最喜歡繪畫興趣的人數為700人;(3)![]()
【解析】
(1)根據頻率=頻數÷總數可得;
(2)總人數乘以A選項對應頻率可得;
(3)根據題意列表,求出所有等可能的結果,再用兩人恰好選中同一類的結果數除以總的結果數即可.
解:(1)a=18÷0.3=60,b=15÷60=0.25,
故答案為60 , 0.25;
(2)估計該市2000名小學生中最喜歡“繪畫”興趣班的人數2000×0.35=700(人);
(3)根據題意列表如下:
王姝 李要 | A | B | C | D |
A | AA | AB | AC | AD |
B | AB | BB | CB | DB |
C | AC | BC | CC | DC |
D | AD | BD | CD | DD |
共有16種等可能的結果,其中兩人恰好選中同一類的結果有4種,
∴兩人恰好選中同一類的概率為:![]() .
.


科目:初中數學 來源: 題型:
【題目】“今有善行者行一百步,不善行者行六十步”(出自《九章算術》)意思是:同樣時間段內,走路快的人能走100步,走路慢的人只能走60步,假定兩者步長相等,據此回答以下問題:
(1)今不善行者先行一百步,善行者追之,不善行者再行六百步,問孰至于前,兩者幾何步隔之?即:走路慢的人先走100步,走路快的人開始追趕,當走路慢的人再走600步時,請問誰在前面,兩人相隔多少步?
(2)今不善行者先行兩百步,善行者追之,問幾何步及之?即:走路慢的人先走200步,請問走路快的人走多少步才能追上走路慢的人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場第一次購進20件A商品,40件B商品,共用了1980元.脫銷后,在進價不變的情況下,第二次購進40件A商品,20件B商品,共用了1560元.商品A的售價為每件30元,商品B的售價為每件60元.
(1)求A,B兩種商品每件的進價分別是多少元?
(2)為了滿足市場需求,需購進A,B兩種商品共1000件,且A種商品的數量不少于B種商品數量的3倍,請你設計進貨方案,使這1000件商品售完后,商場獲利最大,并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
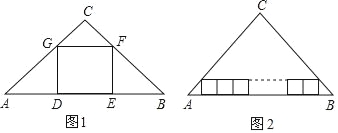
【題目】在△ABC中,∠C=90°,AC=4,BC=3,如圖1,四邊形DEFG為△ABC的內接正方形,則正方形DEFG的邊長為_____.如圖2,若三角形ABC內有并排的n個全等的正方形,它們組成的矩形內接于△ABC,則正方形的邊長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
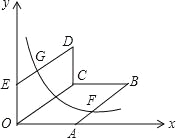
【題目】如圖,0為原點,A(4,0),E(0,3),四邊形OABC,四邊形OCDE都為平行四邊形,OC=5,函數y=![]() (x>0)的圖象經過AB的中點F和DE的中點G,則k的值為 .
(x>0)的圖象經過AB的中點F和DE的中點G,則k的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】哈市某段地鐵工程由甲、乙兩工程隊合作![]() 天可完成.若單獨施工,甲工程隊比乙工程隊多用
天可完成.若單獨施工,甲工程隊比乙工程隊多用![]() 天.
天.
![]() 求甲、乙兩工程隊單獨完成此項工程各需要多少天?
求甲、乙兩工程隊單獨完成此項工程各需要多少天?
![]() 如果甲工程隊施工每天需付施工費
如果甲工程隊施工每天需付施工費![]() 萬元,乙工程隊施工每天需付施工費
萬元,乙工程隊施工每天需付施工費![]() 萬元,甲工程隊最多要單獨施工多少天后,再由甲.乙兩工程隊合作施工完成剩下的工程,才能使施工費不超過
萬元,甲工程隊最多要單獨施工多少天后,再由甲.乙兩工程隊合作施工完成剩下的工程,才能使施工費不超過![]() 萬元?
萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年平昌冬奧會在2月9日到25日在韓國平昌郡舉行,為了調查中學生對冬奧會比賽項目的了解程度,某中學在學生中做了一次抽樣調查,調查結果共分為四個等級:A、非常了解B、比較了解C、基本了解D、不了解.根據調查統計結果,繪制了如圖所示的不完整的三種統計圖表.
對冬奧會了解程度的統計表
對冬奧會的了解程度 | 百分比 |
A非常了解 | 10% |
B比較了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
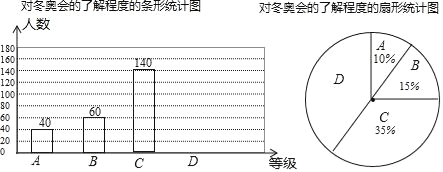
(1)n= ;
(2)扇形統計圖中,D部分扇形所對應的圓心角是 ;
(3)請補全條形統計圖;
(4)根據調查結果,學校準備開展冬奧會的知識競賽,某班要從“非常了解”程度的小明和小剛中選一人參加,現設計了如下游戲來確定誰參賽,具體規則是:把四個完全相同的乒乓球標上數字1,2,3,4然后放到一個不透明的袋中,一個人先從袋中摸出一個球,另一人再從剩下的三個球中隨機摸出一個球,若摸出的兩個球上的數字和為偶數,則小明去,否則小剛去,請用畫樹狀圖或列表的方法說明這個游戲是否公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一驢友分三次從![]() 地出發沿著不同線路(
地出發沿著不同線路(![]() 線、
線、![]() 線、
線、![]() 線)去
線)去![]() 地,在每條線路上行進的方式都分為穿越叢林、涉水行走和攀登這三種.他涉水行走4小時的路程與攀登6小時的路程相等;
地,在每條線路上行進的方式都分為穿越叢林、涉水行走和攀登這三種.他涉水行走4小時的路程與攀登6小時的路程相等;![]() 線、
線、![]() 線路程相等,都比
線路程相等,都比![]() 線路程多
線路程多![]() ;
;![]() 線總時間等于
線總時間等于![]() 線總時間的一半;他用了3小時穿越叢林、2小時涉水行走和2小時攀登走完
線總時間的一半;他用了3小時穿越叢林、2小時涉水行走和2小時攀登走完![]() 線;在
線;在![]() 線中穿越叢林、涉水行走和攀登所用時間分別比
線中穿越叢林、涉水行走和攀登所用時間分別比![]() 線上升了
線上升了![]() .若他用了
.若他用了![]() 小時穿越叢林、
小時穿越叢林、![]() 小時涉水行走和
小時涉水行走和![]() 小時攀登走完
小時攀登走完![]() 線,且
線,且![]() 都為正整數,則
都為正整數,則![]() _____.
_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①所示,已知正方形ABCD和正方形AEFG,連接DG,BE.

(1)發現:當正方形AEFG繞點A旋轉,如圖②所示.
①線段DG與BE之間的數量關系是 ;
②直線DG與直線BE之間的位置關系是 ;
(2)探究:如圖③所示,若四邊形ABCD與四邊形AEFG都為矩形,且AD=2AB,AG=2AE時,上述結論是否成立,并說明理由.
(3)應用:在(2)的情況下,連接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接寫出結果).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com