【題目】如圖，在
中，
，
，
，點
在
邊上，
，
，垂足為
，與
交于點
，則
的長是（ ）
A.1.5B.2.5C.
D.
【答案】B
【解析】
連接DE，由勾股定理求出AB=5，由等腰三角形的性質得出CF=DF，由線段垂直平分線的性質得出CE=DE，由SSS證明△ADE≌△ACE，得出∠ADE=∠ACE=∠BDE=90°，設CE=DE=x，則BE=4-x，在Rt△BDE中，由勾股定理得出方程，解方程即可．
解：連接DE，如圖所示，
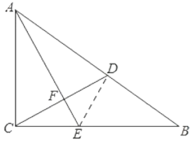
∵在Rt△ABC中，∠ACB=90°，AC=3，BC=4，
∴AB=
，
∵
=3，
，
∴CF=DF
∴CE=DE，BD=AB-AD=2
在△ADE和△ACE中，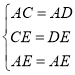
∴△ADE≌△ACE (SSS)
∴∠ADE=∠ACE=90°，
∴∠BDE=90°，
設CE=DE=x，
則BE=4-x，
在Rt△BDE中，由勾股定理得：DE+BD=BE，
即x+2=(4-x)
解得：x=1.5
∴CE=1.5
∴BE=4-1.5=2.5
故選：B
輕松課堂單元期中期末專題沖刺100分系列答案科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AB=8厘米，AC=16厘米，點P從A出發，以每秒2厘米的速度向B運動，點Q從C同時出發，以每秒3厘米的速度向A運動，其中一個動點到端點時，另一個動點也相應停止運動，設運動的時間為t．
⑴用含t的代數式表示：AP= ，AQ= ．
⑵當以A，P，Q為頂點的三角形與△ABC相似時，求運動時間是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
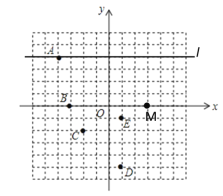
【題目】在平面直角坐標系中，每個小方格的邊長為一個單位長度．
（1）點
的坐標為__________，點
的坐標為__________；
（2）點
關于
軸對稱點的坐標為__________；
（3）在直線
上找一點
，使
為等腰三角形，點坐標為__________
查看答案和解析>>
科目：初中數學 來源： 題型：
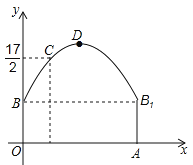
【題目】（12分）如圖所示是隧道的截面由拋物線和長方形構成，長方形的長是12 m，寬是4 m．按照圖中所示的直角坐標系，拋物線可以用y=
x2+bx+c表示，且拋物線上的點C到OB的水平距離為3 m，到地面OA的距離為
m.
（1）求拋物線的函數關系式，并計算出拱頂D到地面OA的距離；
（2）一輛貨運汽車載一長方體集裝箱后高為6m，寬為4m，如果隧道內設雙向車道，那么這輛貨車能否安全通過？
（3）在拋物線型拱壁上需要安裝兩排燈，使它們離地面的高度相等，如果燈離地面的高度不超過8m，那么兩排燈的水平距離最小是多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
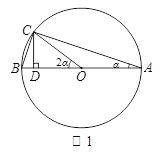
【題目】【閱讀學習】 劉老師提出這樣一個問題：已知α為銳角，且tanα=
，求sin2α的值．
小娟是這樣解決的：
如圖1，在⊙O中，AB是直徑，點C在⊙O上，∠BAC=α，所以∠ACB=90°，tanα=
=．
易得∠BOC=2α．設BC=x，則AC=3x，則AB=
x．作CD⊥AB于D，求出CD= （用含x的式子表示），可求得sin2α=
= ．
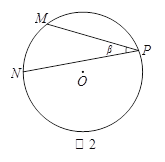
【問題解決】
已知，如圖2，點M、N、P為圓O上的三點，且∠P=β，tanβ =
，求sin2β的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，拋物線y=ax2+bx+c與坐標軸分別交于點A（0，6），B（6，0），C（﹣2，0），點P是線段AB上方拋物線上的一個動點．
（1）求拋物線的解析式；
（2）當點P運動到什么位置時，△PAB的面積有最大值？
（3）過點P作x軸的垂線，交線段AB于點D，再過點P做PE∥x軸交拋物線于點E，連結DE，請問是否存在點P使△PDE為等腰直角三角形？若存在，求出點P的坐標；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
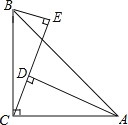
【題目】如圖，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分別為D，E．
(1)求證：△ACD≌△CBE；
(2)若AD=12，DE=7，求BE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=﹣
x2+bx+c的圖象經過A（0，3），B（﹣4，﹣
）兩點．
（1）求b，c的值．
（2）二次函數y=﹣x2+bx+c的圖象與x軸是否有公共點，求公共點的坐標；若沒有，請說明情況．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
