
【題目】已知:如圖,等邊△ABC內接于⊙O,點P是劣弧![]() 上的一點(端點除外),延長BP至D,使BD=AP,連接CD.
上的一點(端點除外),延長BP至D,使BD=AP,連接CD.
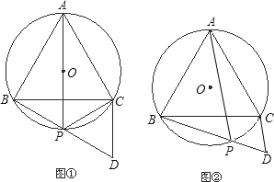
(1)若AP過圓心O,如圖①,請你判斷△PDC是什么三角形?并說明理由;
(2)若AP不過圓心O,如圖②,△PDC又是什么三角形?為什么?
【答案】(1)△PDC為等邊三角形,理由見解析(2)△PDC仍為等邊三角形,理由見解析.
【解析】
試題分析:(1)觀察圖形可得△PDC為等邊三角形,先根據條件證明△APC≌△BDC得出PC=DC,然后根據條件證明∠CPD=60°即可得出結論;(2)利用(1)中方法即可得出結論.
試題解析:(1)如圖①,△PDC為等邊三角形.(2分)
理由如下:
∵△ABC為等邊三角形
∴AC=BC
∵在⊙O中,∠PAC=∠PBC
又∵AP=BD
∴△APC≌△BDC
∴PC=DC
∵AP過圓心O,AB=AC,∠BAC=60°
∴∠BAP=∠PAC=![]() ∠BAC=30°
∠BAC=30°
∴∠PBC=∠PAC=30°,∠BCP=∠BAP=30°
∴∠CPD=∠PBC+∠BCP=30°+30°=60°
∴△PDC為等邊三角形;(6分)
(2)如圖②,△PDC仍為等邊三角形.(8分)
理由如下:
∵△ABC為等邊三角形
∴AC=BC
∵在⊙O中,∠PAC=∠PBC
又∵AP=BD
∴△APC≌△BDC
∴PC=DC
∵∠BAP=∠BCP,∠PBC=∠PAC
∴∠CPD=∠PBC+∠BCP=∠PAC+∠BAP=60°
∴△PDC為等邊三角形.


科目:初中數學 來源: 題型:
【題目】進入冬季,我市空氣質量下降,多次出現霧霾天氣.商場根據市民健康需要,代理銷售一種防塵口罩,進貨價為20元/包,經市場銷售發現:銷售單價為30元/包時,每周可售出200包,每漲價1元,就少售出5包.若供貨廠家規定市場價不得低于30元/包,且商場每周完成不少于150包的銷售任務.
(1)試確定周銷售量y(包)與售價x(元/包)之間的函數關系式;
(2)試確定商場每周銷售這種防塵口罩所獲得的利潤w(元)與售價x(元/包)之間的函數關系式,并直接寫出售價x的范圍;
(3)當售價x(元/包)定為多少元時,商場每周銷售這種防塵口罩所獲得的利潤w(元)最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】本市出租車的收費標準為:3千米以內(含3千米)收費5元,超過3千米的部分每千米收費1.20元(不足1千米按1千米計算),另加收0.60元的返空費.
(1)設行駛路程為x千米(![]() ≥3且取整數),用x表示出應收費y元的代數式;
≥3且取整數),用x表示出應收費y元的代數式;
(2)當收費為10.40元時,該車行駛路程不超過多少千米?路程數在哪個范圍內?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人從少年宮出發,沿相同的路分別以不同的速度勻速跑向體育館,甲先跑一段路程后,乙開始出發,當乙超出甲150米時,乙停在此地等候甲,兩人相遇后乙又繼續以原來的速度跑向體育館.如圖是甲、乙兩人在跑步的全過程中經過的路程y(米)與甲出發的時間x(秒)的函數圖象.
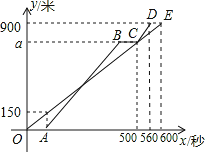
(1)在跑步的全過程中,甲共跑了 米, 甲的速度為 米/秒;
(2)乙跑步的速度是多少?乙在途中等候甲用了多長時間?
(3)甲出發多長時間第一次與乙相遇?此時乙跑了多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛貨車從百貨大樓出發負責送貨,向東走了4千米到達小明家,繼續向東走了1.5千米到達小紅家,然后向西走了8.5千米到達小剛家,最后返回百貨大樓.
(1)以百貨大樓為原點,向東為正方向,1個單位長度表示1千米,請你在數軸上標出小明、小紅、小剛家的位置.(小明家用點A表示,小紅家用點B表示,小剛家用點C表示)
![]()
(2)小明家與小剛家相距多遠?
(3)若貨車每千米耗油1.5升,那么這輛貨車此次送貨共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面有8個算式,排成4行2列
2+2, 2×2
3+![]() , 3×
, 3×![]()
4+![]() , 4×
, 4×![]()
5+![]() , 5×
, 5×![]()
……, ……
(1)同一行中兩個算式的結果怎樣?
(2)算式2005+![]() 和2005×
和2005×![]() 的結果相等嗎?
的結果相等嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】金瑞公司決定從廠家購進甲、乙兩種不同型號的顯示器共50臺,購進顯示器的總金額不超過77000元,已知甲、乙型號的顯示器價格分別為1000元/臺、2000元/臺.
(1)求金瑞公司至少購進甲型顯示器多少臺?
(2)若甲型顯示器的臺數不超過乙型顯示器的臺數,則有哪些購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=![]() 交x軸于點A、B,交y軸于點C,點A的坐標是(-1,0),點C的坐標是(0,2).
交x軸于點A、B,交y軸于點C,點A的坐標是(-1,0),點C的坐標是(0,2).
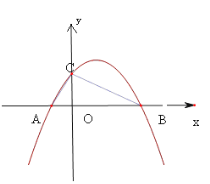
(1)求該拋物線的解析式。
(2)已知點P是拋物線上的一個動點,點N在x軸上。
①若點P在x軸上方,且△APN是等腰直角三角形,求點N的坐標;
②若點P在x軸下方,且△APN∽△BOC,請直接寫出點N的坐標。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com