
題目列表(包括答案和解析)
(本題9分)給出下面的數(shù)表序列:
|
表1 |
表2 |
表3 |
… |
|
1 |
1 3 |
1 3 5 |
|
|
|
4 |
4 8 |
|
|
|
|
12 |
|
其中表 有
有 行,第1行的
行,第1行的 個(gè)數(shù)是1,3,5,…,
個(gè)數(shù)是1,3,5,…, ,從第2行起,每行中的每個(gè)數(shù)都等于它肩上的兩數(shù)之和。
,從第2行起,每行中的每個(gè)數(shù)都等于它肩上的兩數(shù)之和。
(1)寫出表4,驗(yàn)證表4各行中數(shù)的平均數(shù)按從上到下的順序構(gòu)成等比數(shù)列,并將結(jié)論推廣到表 (不要求證明)
(不要求證明)
(2)每個(gè)數(shù)表中最后一行都只有一個(gè)數(shù),它們構(gòu)成數(shù)列1,4,12,…,記此數(shù)列為 ,求數(shù)列
,求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和
(本題9分)給出下面的數(shù)表序列:
| 表1 | 表2 | 表3 | … |
| 1 | 1 3 | 1 3 5 | |
| | 4 | 4 8 | |
| | | 12 | |
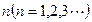 有
有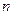 行,第1行的
行,第1行的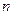 個(gè)數(shù)
個(gè)數(shù) 是1,3,5,…,
是1,3,5,…, ,從第2行起,每行中的每個(gè)數(shù)都等于它肩上的兩數(shù)之和。
,從第2行起,每行中的每個(gè)數(shù)都等于它肩上的兩數(shù)之和。 (不要求證明)
(不要求證明)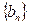 ,求數(shù)列
,求數(shù)列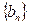 的前
的前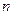 項(xiàng)和
項(xiàng)和
學(xué)習(xí)三角函數(shù)一章時(shí),課堂上老師給出這樣一個(gè)結(jié)論:當(dāng)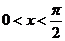 時(shí),有
時(shí),有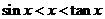 恒成立,當(dāng)老師把這個(gè)證明完成時(shí),
恒成立,當(dāng)老師把這個(gè)證明完成時(shí),
(Ⅰ) 學(xué)生甲提出問題:能否在不等式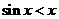 的左邊增加一個(gè)量,使不等號的方向得以改變?
的左邊增加一個(gè)量,使不等號的方向得以改變?
下面請同學(xué)們證明:若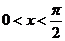 ,則
,則
 成立。
成立。
(Ⅱ) 當(dāng)學(xué)生甲的問題完成時(shí),學(xué)生乙提問:對于不等式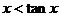 是否也有相似的結(jié)論?
是否也有相似的結(jié)論?
下面請同學(xué)們探討:若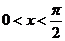 ,是否存在實(shí)數(shù)
,是否存在實(shí)數(shù)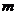 ,使
,使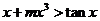 恒成立?如果存在,求出
恒成立?如果存在,求出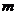 的一個(gè)值;如果不存在,請說明理由.
的一個(gè)值;如果不存在,請說明理由.
學(xué)習(xí)三角函數(shù)一章時(shí),課堂上老師給出這樣一個(gè)結(jié)論:當(dāng)![]() 時(shí),有
時(shí),有![]() 恒成立,當(dāng)老師把這個(gè)證明完成時(shí),
恒成立,當(dāng)老師把這個(gè)證明完成時(shí),
(Ⅰ) 學(xué)生甲提出問題:能否在不等式![]() 的左邊增加一個(gè)量,使不等號的方向得以改變?
的左邊增加一個(gè)量,使不等號的方向得以改變?
下面請同學(xué)們證明:若![]() ,則
,則 ![]() 成立。
成立。
(Ⅱ) 當(dāng)學(xué)生甲的問題完成時(shí),學(xué)生乙提問:對于不等式![]() 是否也有相似的結(jié)論?
是否也有相似的結(jié)論?
下面請同學(xué)們探討:若![]() ,是否存在實(shí)數(shù)
,是否存在實(shí)數(shù)![]() ,使
,使![]() 恒成立?如果存在,求出
恒成立?如果存在,求出![]() 的一個(gè)值;如果不存在,請說明理由.
的一個(gè)值;如果不存在,請說明理由.
學(xué)習(xí)三角函數(shù)一章時(shí),課堂上老師給出這樣一個(gè)結(jié)論:當(dāng)![]() 時(shí),有
時(shí),有![]() 恒成立,當(dāng)老師把這個(gè)證明完成時(shí),
恒成立,當(dāng)老師把這個(gè)證明完成時(shí),
(Ⅰ) 學(xué)生甲提出問題:能否在不等式![]() 的左邊增加一個(gè)量,使不等號的方向得以改變?下面請同學(xué)們證明:若
的左邊增加一個(gè)量,使不等號的方向得以改變?下面請同學(xué)們證明:若![]() ,則
,則 ![]() 成立;
成立;
(Ⅱ) 當(dāng)學(xué)生甲的問題完成時(shí),學(xué)生乙提問:對于不等式![]() 是否也有相似的結(jié)論?下面請同學(xué)們探討:若
是否也有相似的結(jié)論?下面請同學(xué)們探討:若![]() ,是否存在實(shí)數(shù)
,是否存在實(shí)數(shù)![]() ,使
,使![]() 恒成立?如果存在,求出
恒成立?如果存在,求出![]() 的一個(gè)值;如果不存在,請說明理由。
的一個(gè)值;如果不存在,請說明理由。
一、選擇題
CCCBB BBDAB CA
二、填空題
13、年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image180.gif) 14、2 15、
14、2 15、年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image182.gif) 16、③④
16、③④
三、解答題
17.解:年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image184.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image186.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image188.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image190.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image192.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image194.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image196.gif)
建議評分標(biāo)準(zhǔn):每個(gè)三角函數(shù)“1”分。(下面的評分標(biāo)準(zhǔn)也僅供參考)
18.解:年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image198.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image140.gif) =
=年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image200.gif) =
=年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image202.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image204.gif) --(2分)
--(2分)
而年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image206.gif) =
=年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image208.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image210.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image212.gif) ----------------------------------------------------------(2分)
----------------------------------------------------------(2分)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image214.gif) 且
且年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image216.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image218.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image220.gif) -----(2分)
-----(2分) 年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image210.gif) 原式=
原式=年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image223.gif) -------------(2分)
-------------(2分)
19.解:(1)由已知得年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image225.gif) ,所以
,所以年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image227.gif) 即三角形為等腰三角形。--------------------------------------------------------------------------------------------(3分)
即三角形為等腰三角形。--------------------------------------------------------------------------------------------(3分)
(2)兩式平方相加得年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image229.gif) ,所以
,所以年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image231.gif) 。------(3分)
。------(3分)
若年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image233.gif) ,則
,則年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image235.gif) ,所以
,所以年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image237.gif) ,而
,而年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image239.gif)
這與年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image148.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image150.gif) 矛盾,所以
矛盾,所以年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image241.gif) ---------------------------------------(2分)
---------------------------------------(2分)
20.解:化簡得年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image243.gif) --------------------------------------------------(2分)
--------------------------------------------------(2分)
(1)最小正周期為年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image037.gif) ;--------------------------------------------------------------(2分)
;--------------------------------------------------------------(2分)
(2)單調(diào)遞減區(qū)間為年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image246.gif) -------------------------------(2分)
-------------------------------(2分)
(3)對稱軸方程為年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image248.gif) -------------------------------------------(1分)
-------------------------------------------(1分)
對稱中心為年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image250.gif) ------------------------------------------------------(1分)
------------------------------------------------------(1分)
21.對方案Ⅰ:連接OC,設(shè)年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image252.gif) ,則
,則年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image254.gif) ,
,年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image256.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image258.gif) 而
而年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image260.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image262.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image210.gif) 當(dāng)
當(dāng)年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image265.gif) ,即點(diǎn)C為弧的中點(diǎn)時(shí),矩形面積為最大,等于
,即點(diǎn)C為弧的中點(diǎn)時(shí),矩形面積為最大,等于年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image267.gif) 。
。
對方案Ⅱ:取弧EF的中點(diǎn)P,連接OP,交CD于M,交AB于N,設(shè)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image269.gif) 如圖所示。
如圖所示。
則年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image271.gif) ,
,年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image273.gif) ,
,年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image275.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image277.gif)
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image279.gif)
所以當(dāng)年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image281.gif) ,即點(diǎn)C為弧EF的四等分點(diǎn)時(shí),矩形面積為最大,等于
,即點(diǎn)C為弧EF的四等分點(diǎn)時(shí),矩形面積為最大,等于年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image283.gif) 。
。
年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image285.gif) ,所以選擇方案Ⅰ。
,所以選擇方案Ⅰ。
22.解:(1)不是休閑函數(shù),證明略
(2)由題意得,年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image287.gif) 有解,顯然
有解,顯然年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image289.gif) 不是解,所以存在非零常數(shù)T,使
不是解,所以存在非零常數(shù)T,使年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image291.gif) ,
,
于是有年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image293.gif) ,所以
,所以年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image174.gif) 是休閑函數(shù)。
是休閑函數(shù)。
(3)顯然年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image296.gif) 時(shí)成立;
時(shí)成立;
當(dāng)年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image298.gif) 時(shí),由題義,
時(shí),由題義,年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image300.gif) ,由值域考慮,只有
,由值域考慮,只有年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image302.gif) ,
,
當(dāng)年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image304.gif) 時(shí),
時(shí),年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image306.gif) 成立,則
成立,則年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image308.gif) ;
;
當(dāng)年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image310.gif) 時(shí),
時(shí),年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image312.gif) 成立,則
成立,則年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image314.gif) ,綜合的
,綜合的年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image178.gif) 的取值為
的取值為年度第二學(xué)期期中杭州地區(qū)七校聯(lián)考試卷高一數(shù)學(xué).files\image317.gif) 。
。
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com