
題目列表(包括答案和解析)
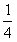 ,tanB=
,tanB=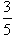 ,
,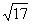 ,求BC邊的長。
,求BC邊的長。 在△ABC中, ,
,
(1)求角C的大小;
(2)若△ABC最大邊的邊長為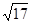 ,求最小邊的邊長。
,求最小邊的邊長。
在△ABC中,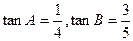 ,
,
(1)求角C的大小;
(2)若△ABC最大邊的邊長為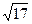 ,求最小邊的邊長。
,求最小邊的邊長。
在△ABC中,![]() ,
,
(1)求角C的大小;
(2)若△ABC最大邊的邊長為![]() ,求最小邊的邊長。
,求最小邊的邊長。
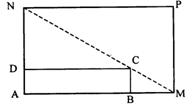
如圖所示,將一矩形花壇![]() 擴建成一個更大的矩形花園
擴建成一個更大的矩形花園![]() ,要求B在
,要求B在![]() 上,D在
上,D在![]() 上,且對角線
上,且對角線![]() 過C點,已知AB=3米,AD=2米,
過C點,已知AB=3米,AD=2米,
(1)要使矩形![]() 的面積大于32平方米,則
的面積大于32平方米,則![]() 的長應在什么范圍內?
的長應在什么范圍內?
(2)若![]() 的長度不少于6米,則當
的長度不少于6米,則當![]() 的長度是多少時,矩形
的長度是多少時,矩形![]() 的面積最小?并求出最小面積。
的面積最小?并求出最小面積。
 |
![]()
一、選擇題
CCCBB BBDAB CA
二、填空題
13、 14、2 15、
14、2 15、 16、③④
16、③④
三、解答題
17.解:






建議評分標準:每個三角函數“1”分。(下面的評分標準也僅供參考)
18.解:
 =
= =
=
 --(2分)
--(2分)
而 =
=

 ----------------------------------------------------------(2分)
----------------------------------------------------------(2分)
 且
且

 -----(2分)
-----(2分)  原式=
原式= -------------(2分)
-------------(2分)
19.解:(1)由已知得 ,所以
,所以 即三角形為等腰三角形。--------------------------------------------------------------------------------------------(3分)
即三角形為等腰三角形。--------------------------------------------------------------------------------------------(3分)
(2)兩式平方相加得 ,所以
,所以 。------(3分)
。------(3分)
若 ,則
,則 ,所以
,所以 ,而
,而
這與
 矛盾,所以
矛盾,所以 ---------------------------------------(2分)
---------------------------------------(2分)
20.解:化簡得 --------------------------------------------------(2分)
--------------------------------------------------(2分)
(1)最小正周期為 ;--------------------------------------------------------------(2分)
;--------------------------------------------------------------(2分)
(2)單調遞減區間為 -------------------------------(2分)
-------------------------------(2分)
(3)對稱軸方程為 -------------------------------------------(1分)
-------------------------------------------(1分)
對稱中心為 ------------------------------------------------------(1分)
------------------------------------------------------(1分)
21.對方案Ⅰ:連接OC,設 ,則
,則 ,
,
 而
而

 當
當 ,即點C為弧的中點時,矩形面積為最大,等于
,即點C為弧的中點時,矩形面積為最大,等于 。
。
對方案Ⅱ:取弧EF的中點P,連接OP,交CD于M,交AB于N,設
 如圖所示。
如圖所示。
則 ,
, ,
,


所以當 ,即點C為弧EF的四等分點時,矩形面積為最大,等于
,即點C為弧EF的四等分點時,矩形面積為最大,等于 。
。
 ,所以選擇方案Ⅰ。
,所以選擇方案Ⅰ。
22.解:(1)不是休閑函數,證明略
(2)由題意得, 有解,顯然
有解,顯然 不是解,所以存在非零常數T,使
不是解,所以存在非零常數T,使 ,
,
于是有 ,所以
,所以 是休閑函數。
是休閑函數。
(3)顯然 時成立;
時成立;
當 時,由題義,
時,由題義, ,由值域考慮,只有
,由值域考慮,只有 ,
,
當 時,
時, 成立,則
成立,則 ;
;
當 時,
時, 成立,則
成立,則 ,綜合的
,綜合的 的取值為
的取值為 。
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com