相關習題
0 108906 108914 108920 108924 108930 108932 108936 108942 108944 108950 108956 108960 108962 108966 108972 108974 108980 108984 108986 108990 108992 108996 108998 109000 109001 109002 109004 109005 109006 109008 109010 109014 109016 109020 109022 109026 109032 109034 109040 109044 109046 109050 109056 109062 109064 109070 109074 109076 109082 109086 109092 109100 266669
科目:
來源:2009年廣東省高考數學試卷(理科)(解析版)
題型:解答題
已知曲線C
n:x
2-2nx+y
2=0(n=1,2,…).從點P(-1,0)向曲線C
n引斜率為k
n(k
n>0)的切線l
n,切點為P
n(x
n,y
n).
(1)求數列{x
n}與{y
n}的通項公式;
(2)證明:
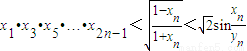
.
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
用錘子以均勻的力敲擊鐵釘釘入木板.隨著鐵釘的深入,鐵釘所受的阻力會越來越大,使得每次釘入木板的釘子長度后一次為前一次的
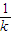
(k∈N
*).已知一個鐵釘受擊3次后全部進入木板,且第一次受擊后進入木板部分的鐵釘長度是釘長的

,請從這件事實中提煉出一個不等式組是
.
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
已知P={x|1≤x≤9,x∈N},記f(a,b,c,d)=ab-cd,(其中a,b,c,d∈P),例如:f(1,2,3,4)=1×2-3×4=-10.設u,v,x,y∈P,且滿足f(u,v,x,y)=39和f(u,y,x,v)=66,則有序數組(u,v,x,y)是 .
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
有窮數列{a
n},S
n為其前n項和,定義T
n=
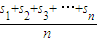
為數列{a
n}的“凱森和”,如果有99項的數列a
1、a
2、a
3、…、a
99的“凱森和”為1000,則有100項的數列1、a
1、a
2、a
3、…、a
99的“凱森和”T
100=
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
如圖,點P在⊙O的直徑BA的延長線上,AB=2PA,PC切⊙O于點C,連接BC.
(1)求∠P的正弦值;
(2)若⊙O的半徑r=2cm,求BC的長度.
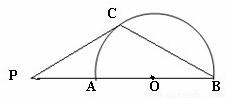
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
若AB是過二次曲線中心的任一條弦,M是二次曲線上異于A、B的任一點,且AM、BM均與坐標軸不平行,則對于橢圓
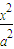

=1有K
AM•K
BM=-
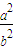
.類似地,對于雙曲線
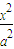
-
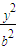
=1有K
AM•K
BM=
.
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
已知x、y之間滿足
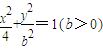
(1)方程
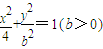
表示的曲線經過一點
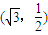
,求b的值
(2)(理做文不做)動點(x,y)在曲線

(b>0)上變化,求x
2+2y的最大值.
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
設P表示冪函數

在(0,+∞)上是增函數的c的集合;Q表示不等式|x-1|+|x-4|≥c對任意x∈R恒成立的c的集合.
(1)求P∪Q;
(2)試寫出一個解集為P∪Q的不等式.
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
已知f(x)=a
2x-

x
3,x∈(-2,2)為正常數.
(1)可以證明:定理“若a、b∈R
*,則


(當且僅當a=b時取等號)”推廣到三個正數時結論是正確的,試寫出推廣后的結論(無需證明);
(2)若f(x)>0在(0,2)上恒成立,且函數f(x)的最大值大于1,求實數a的取值范圍,并由此猜測y=f(x)的單調性(無需證明);
(3)對滿足(2)的條件的一個常數a,設x=x
1時,f(x)取得最大值.試構造一個定義在D={x|x>-2,且x≠4k-2,k∈N}上的函數g(x),使當x∈(-2,2)時,g(x)=f(x),當x∈D時,g(x)取得最大值的自變量的值構成以x
1為首項的等差數列.
查看答案和解析>>
科目:
來源:2010年高考數學新題型解析選編(4)(解析版)
題型:解答題
已知函數f(x)=ax
2-2
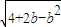
x,g(x)=-
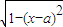
,(a,b∈R)
(Ⅰ)當b=0時,若f(x)在[2,+∞)上單調遞增,求a的取值范圍;
(Ⅱ)求滿足下列條件的所有實數對(a,b):當a是整數時,存在x
,使得f(x
)是f(x)的最大值,g(x
)是g(x)的最小值.
查看答案和解析>>

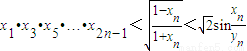 .
.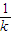 (k∈N*).已知一個鐵釘受擊3次后全部進入木板,且第一次受擊后進入木板部分的鐵釘長度是釘長的
(k∈N*).已知一個鐵釘受擊3次后全部進入木板,且第一次受擊后進入木板部分的鐵釘長度是釘長的 ,請從這件事實中提煉出一個不等式組是 .
,請從這件事實中提煉出一個不等式組是 .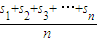 為數列{an}的“凱森和”,如果有99項的數列a1、a2、a3、…、a99的“凱森和”為1000,則有100項的數列1、a1、a2、a3、…、a99的“凱森和”T100=
為數列{an}的“凱森和”,如果有99項的數列a1、a2、a3、…、a99的“凱森和”為1000,則有100項的數列1、a1、a2、a3、…、a99的“凱森和”T100= 
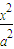
 =1有KAM•KBM=-
=1有KAM•KBM=-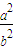 .類似地,對于雙曲線
.類似地,對于雙曲線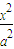 -
-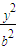 =1有KAM•KBM= .
=1有KAM•KBM= .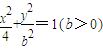
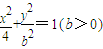 表示的曲線經過一點
表示的曲線經過一點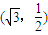 ,求b的值
,求b的值 (b>0)上變化,求x2+2y的最大值.
(b>0)上變化,求x2+2y的最大值. 在(0,+∞)上是增函數的c的集合;Q表示不等式|x-1|+|x-4|≥c對任意x∈R恒成立的c的集合.
在(0,+∞)上是增函數的c的集合;Q表示不等式|x-1|+|x-4|≥c對任意x∈R恒成立的c的集合. x3,x∈(-2,2)為正常數.
x3,x∈(-2,2)為正常數.
 (當且僅當a=b時取等號)”推廣到三個正數時結論是正確的,試寫出推廣后的結論(無需證明);
(當且僅當a=b時取等號)”推廣到三個正數時結論是正確的,試寫出推廣后的結論(無需證明);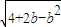 x,g(x)=-
x,g(x)=-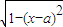 ,(a,b∈R)
,(a,b∈R)