
【題目】已知函數f(x)=cos(ωx+ ![]() ),(ω>0,0<φ<π),其中x∈R且圖象相鄰兩對稱軸之間的距離為
),(ω>0,0<φ<π),其中x∈R且圖象相鄰兩對稱軸之間的距離為 ![]() ;
;
(1)求f(x)的對稱軸方程和單調遞增區間;
(2)求f(x)的最大值、最小值,并指出f(x)取得最大值、最小值時所對應的x的集合.
【答案】
(1)解:函數f(x)=cos(ωx+ ![]() )的圖象的兩對稱軸之間的距離為
)的圖象的兩對稱軸之間的距離為 ![]() =
= ![]() ,
,
∴ω=2,f(x)=cos(2x+ ![]() ).
).
令2x+ ![]() =kπ,求得x=
=kπ,求得x= ![]() ﹣
﹣ ![]() ,可得對稱軸方程為 x=
,可得對稱軸方程為 x= ![]() ﹣
﹣ ![]() ,k∈Z.
,k∈Z.
令2kπ﹣π≤2x+ ![]() ≤2kπ,求得 kπ﹣
≤2kπ,求得 kπ﹣ ![]() ≤x≤kπ﹣
≤x≤kπ﹣ ![]() ,
,
可得函數的增區間為[kπ﹣ ![]() ,kπ﹣
,kπ﹣ ![]() ],k∈Z
],k∈Z
(2)解:當2x+ ![]() =2kπ,即x=kπ﹣
=2kπ,即x=kπ﹣ ![]() ,k∈Z時,f(x)取得最大值為1.
,k∈Z時,f(x)取得最大值為1.
當2x+ ![]() =2kπ+π,即x=kπ+
=2kπ+π,即x=kπ+ ![]() ,k∈Z時,f(x)取得最小值為﹣1.
,k∈Z時,f(x)取得最小值為﹣1.
∴f(x)取最大值時相應的x集合為{x|x=kπ﹣ ![]() ,k∈Z};
,k∈Z};
f(x)取最小值時相應的x集合為{x|x=kπ+ ![]() ,k∈Z}
,k∈Z}
【解析】(1)由條件利用余弦函數的圖象特征,求得ω的值,可得函數的解析式,再利用余弦函數的單調性得出結論.(2)由條件利用余弦函數的最值,求得f(x)取得最大值、最小值時所對應的x的集合.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點. 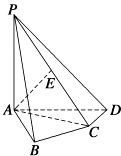
(1)求PB和平面PAD所成的角的大小;
(2)證明:AE⊥平面PCD;
(3)求二面角A﹣PD﹣C得到正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題: ①把函數y=sin(x﹣ ![]() )圖象上所有點的橫坐標縮短到原來的
)圖象上所有點的橫坐標縮短到原來的 ![]() 倍,縱坐標不變,得到函數y=sin(2x﹣
倍,縱坐標不變,得到函數y=sin(2x﹣ ![]() );
);
②若α,β是第一象限角且α<β,則cosα>cosβ;
③x=﹣ ![]() 是函數y=cos(2x+
是函數y=cos(2x+ ![]() π)的一條對稱軸;
π)的一條對稱軸;
④函數y=4sin(2x+ ![]() )與函數y=4cos(2x﹣
)與函數y=4cos(2x﹣ ![]() )相同;
)相同;
⑤y=2sin(2x﹣ ![]() )在[0,
)在[0, ![]() ]是增函數;
]是增函數;
則正確命題的序號 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司對新研發的一種產品進行合理定價,且銷量與單價具有相關關系,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價x(單位:元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y(單位:萬件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)現有三條y對x的回歸直線方程: ![]() =﹣10x+170;
=﹣10x+170; ![]() =﹣20x+250;
=﹣20x+250; ![]() =﹣15x+210;根據所學的統計學知識,選擇一條合理的回歸直線,并說明理由.
=﹣15x+210;根據所學的統計學知識,選擇一條合理的回歸直線,并說明理由.
(2)預計在今后的銷售中,銷量與單價服從(1)中選出的回歸直線方程,且該產品的成本是每件5元,為使公司獲得最大利潤,該產品的單價應定多少元?(利潤=銷售收入﹣成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在物理實驗中,為了研究所掛物體的重量x對彈簧長度y的影響.某學生通過實驗測量得到物體的重量與彈簧長度的對比表:
物體重量(單位g) | 1 | 2 | 3 | 4 | 5 |
彈簧長度(單位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
參考公式:
①.樣本數據x1 , x2 , …xn的標準差
s= ![]() ,其中
,其中 ![]() 為樣本的平均數;
為樣本的平均數;
②.線性回歸方程系數公式 ![]() =
= 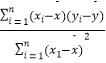 =
= 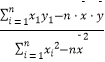 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
(1)畫出散點圖;
(2)利用所給的參考公式,求y對x的回歸直線方程;
(3)預測所掛物體重量為8g時的彈簧長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2bx+c,且f(1)=f(3)=﹣1.設a>0,將函數f(x)的圖像先向右平移a個單位長度,再向下平移a2個單位長度,得到函數g(x)的圖像. (Ⅰ)若函數g(x)有兩個零點x1 , x2 , 且x1<4<x2 , 求實數a的取值范圍;
(Ⅱ)設連續函數在區間[m,n]上的值域為[λ,μ],若有 ![]() ,則稱該函數為“陡峭函數”.若函數g(x)在區間[a,2a]上為“陡峭函數”,求實數a的取值范圍.
,則稱該函數為“陡峭函數”.若函數g(x)在區間[a,2a]上為“陡峭函數”,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com