
【題目】(本小題滿分14分))
某蔬菜基地種植西紅柿,由歷年市場行情得知,從二月一日起的300天內,西紅柿場售價與上市時間的關系用圖一的一條折線表示;西紅柿的種植成本與上市時間的關系用圖二的拋物線段表示。
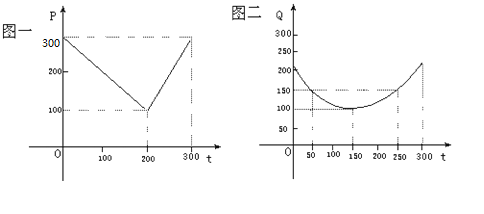
(Ⅰ)寫出圖一表示的市場售價與時間的函數關系式![]() ;寫出圖二表示的種植成本與上市時間的函數關系式
;寫出圖二表示的種植成本與上市時間的函數關系式![]() ;
;
(Ⅱ)假如設定市場售價減去種植成本為純收益,問何時上市的西紅柿純收益最大?(注:市場售價和種植成本的單位:元/102㎏,時間單位:天)
【答案】(1)![]()
![]()
(2)從二月一日開始的第50天時,上市的西紅柿純收益最大
【解析】
試題分析:本題是函數應用題,(1)函數關系式形式題中已經給出,![]() 是分估函數,圖象是兩段線段,一次函數的形式,分別求出即可,
是分估函數,圖象是兩段線段,一次函數的形式,分別求出即可,![]() 是拋物線,二次函數,解析式可設為一般式或頂點式;(2)由(1)可得純收益
是拋物線,二次函數,解析式可設為一般式或頂點式;(2)由(1)可得純收益![]() ,仍是分段函數,其最大值要分段求出,再取最大的一個.
,仍是分段函數,其最大值要分段求出,再取最大的一個.
試題解析:(1)由圖1可得市場售價與時間的函數關系為![]()
由圖2可得種植成本與時間的函數關系為![]()

(2)設![]() 時刻的純收益為
時刻的純收益為![]() ,則由題意得
,則由題意得![]() ,
,
即
當![]() 時,配方整理,得
時,配方整理,得![]()
∴當![]() 時,
時,![]() 取得區間
取得區間![]() 上的最大值100;
上的最大值100;
當![]() 時,配方整理,得
時,配方整理,得![]()
∴當![]() 時,
時,![]() 取得區間
取得區間![]() 上的最大值87.5;
上的最大值87.5;
綜上可知![]() 在區間
在區間![]() 上可以取到最大值100,此時,
上可以取到最大值100,此時,![]() ,即從二月一日開始的第50天時,上市的西紅柿收益最大100。
,即從二月一日開始的第50天時,上市的西紅柿收益最大100。


科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的公差d≠0,它的前n項和為Sn,若S5=70,且a2,a7,a22成等比數列.
(1)求數列{an}的通項公式;
(2)設數列![]() 的前n項和為Tn,求證:
的前n項和為Tn,求證: ![]() ≤Tn<
≤Tn<![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題![]() “存在
“存在![]() ”,命題
”,命題![]() :“曲線
:“曲線![]() 表示焦點在
表示焦點在![]() 軸上的橢圓”,命題
軸上的橢圓”,命題![]() “曲線
“曲線![]() 表示雙曲線”
表示雙曲線”
(1)若“![]() 且
且![]() ”是真命題,求實數
”是真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() 是
是![]() 的必要不充分條件,求實數
的必要不充分條件,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
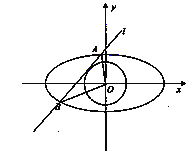
【題目】如圖,直線![]() 與圓O:
與圓O: ![]() 且與橢圓C:
且與橢圓C: ![]() 相交于A,B兩點
相交于A,B兩點
(1)若直線![]() 恰好經過橢圓的左頂點,求弦長AB;
恰好經過橢圓的左頂點,求弦長AB;
(2)設直線OA,OB的斜率分別為k1,k2,判斷k1·k2是否為定值,并說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 的最小正周期與單調遞減區間;
的最小正周期與單調遞減區間;
(2)若函數![]() 的圖象上的所有點的橫坐標伸長到原來的
的圖象上的所有點的橫坐標伸長到原來的![]() 倍,所得的圖象與直線
倍,所得的圖象與直線![]() 交點的橫坐標由小到大依次是
交點的橫坐標由小到大依次是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(14分)關于x的不等式ax2+(a﹣2)x﹣2≥0(a∈R)
(1)已知不等式的解集為(﹣∞,﹣1]∪[2,+∞),求a的值;
(2)解關于x的不等式ax2+(a﹣2)x﹣2≥0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐S﹣ABC的各頂點都在一個半徑為r的球面上,且SA=SB=SC=1,AB=BC=AC=![]() ,則球的表面積為( )
,則球的表面積為( )
A. 12π B. 8π C. 4π D. 3π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn=2n2,{bn}為等比數列,且a1=b1,b2(a2-a1)=b1.
(1)求數列{an}和{bn}的通項公式;
(2)設cn=![]() ,求數列{cn}的前n項和Tn.
,求數列{cn}的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com