
【題目】若存在正數x,y,使得![]() ,其中e為自然對數的底數,則實數
,其中e為自然對數的底數,則實數![]() 的取值范圍是_____________.
的取值范圍是_____________.
【答案】(![]() ,0)
,0)![]() [
[![]() ,
,![]() )
)
【解析】
根據函數與方程的關系將方程進行轉化,利用換元法轉化為方程有解,構造函數求函數的導數,利用函數極值和單調性的關系進行求解即可.
由![]() 得x+s(y﹣2ex)ln
得x+s(y﹣2ex)ln![]() =0,
=0,
即1+s(![]() ﹣2e)ln
﹣2e)ln![]() =0,
=0,
即設t=![]() ,則t>0,
,則t>0,
則條件等價為1+s(t﹣2e)lnt=0,
即(t﹣2e)lnt=![]() 有解,
有解,
設g(t)=(t﹣2e)lnt,
g′(t)=lnt+1﹣![]() 為增函數,
為增函數,
∵g′(e)=lne+1﹣![]() =1+1﹣2=0,
=1+1﹣2=0,
∴當t>e時,g′(t)>0,
當0<t<e時,g′(t)<0,
即當t=e時,函數g(t)取得極小值,為g(e)=(e﹣2e)lne=﹣e,
即g(t)≥g(e)=﹣e,
若(t﹣2e)lnt=![]() 有解,
有解,
則![]() ≥﹣e,即
≥﹣e,即![]() ≤e,
≤e,
則s<0或s≥![]() ,
,
故答案為:s<0或s≥![]() .
.


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:
【題目】如圖,在P地正西方向8km的A處和正東方向1km的B處各有一條正北方向的公路AC和BD,現計劃在AC和BD路邊各修建一個物流中心E和F,為緩解交通壓力,決定修建兩條互相垂直的公路PE和PF,設![]()
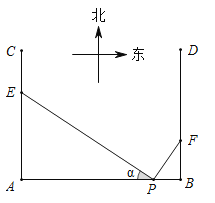
![]() Ⅰ
Ⅰ![]() 為減少對周邊區域的影響,試確定E,F的位置,使
為減少對周邊區域的影響,試確定E,F的位置,使![]() 與
與![]() 的面積之和最小;
的面積之和最小;
![]() Ⅱ
Ⅱ![]() 為節省建設成本,求使
為節省建設成本,求使![]() 的值最小時AE和BF的值.
的值最小時AE和BF的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為![]() ,已知
,已知![]() 且
且![]() .
.
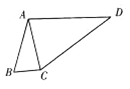
(1)求角![]() ;
;
(2)如圖,D為△ABC外一點,若在平面四邊形ABCD中,![]() ,求△ACD面積的最大值.
,求△ACD面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線M:![]() 的左、右頂點分別為A,B,設P是曲線M上的任意一點.
的左、右頂點分別為A,B,設P是曲線M上的任意一點.
(1)當P異于A,B時,記直線PA、PB的斜率分別為![]() 、
、![]() 則
則![]() 是否為定值,請說明理由.
是否為定值,請說明理由.
(2)已知點C在曲線M長軸上(異于A、B兩點),且![]() 的最大值為7,求點C的坐標.
的最大值為7,求點C的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記![]() (
(![]() ,
,![]() ).
).
(1)求函數![]() 的零點;
的零點;
(2)設![]() 、
、![]() 、
、![]() 均為正整數,且
均為正整數,且![]() 為最簡根式,若存在
為最簡根式,若存在![]() ,使得
,使得![]() 可唯一表示為
可唯一表示為![]() 的形式(
的形式(![]() ),求證:
),求證:![]() ;
;
(3)已知![]() ,是否存在
,是否存在![]() ,使得
,使得![]()
成立,若存在,試求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了預防流感,某學校對教室用藥熏消毒法進行消毒.已知藥物釋放過程中,室內每立方米空氣的含藥量![]() (毫克)與時間
(毫克)與時間![]() (小時)成正比.藥物釋放完畢后,
(小時)成正比.藥物釋放完畢后,![]() 與
與![]() 的函數關系式為
的函數關系式為![]() (
(![]() 為常數),如圖所示,根據圖中提供的信息,回答下列問題:
為常數),如圖所示,根據圖中提供的信息,回答下列問題:

(1)求從藥物釋放開始,每立方米空氣中的含藥量![]() (毫克)與時間
(毫克)與時間![]() (小時)之間的函數關系式;
(小時)之間的函數關系式;
(2)據測定,當空氣中每立方米空氣的含藥量降到0.25毫克以下時,學生方可進教室,那從藥物釋放開始,至少需要經過多少小時后,學生才能回到進教室?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓O:![]() 與坐標軸分別交于A1,A2,B1,B2(如圖).
與坐標軸分別交于A1,A2,B1,B2(如圖).
(1)點Q是圓O上除A1,A2外的任意點(如圖1),直線A1Q,A2Q與直線![]() 交于不同的兩點M,N,求線段MN長的最小值;
交于不同的兩點M,N,求線段MN長的最小值;
(2)點P是圓O上除A1,A2,B1,B2外的任意點(如圖2),直線B2P交x軸于點F,直線A1B2交A2P于點E.設A2P的斜率為k,EF的斜率為m,求證:2m﹣k為定值.
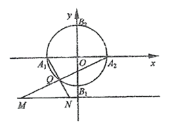
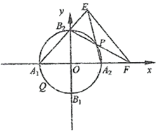
(圖1) (圖2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:如果數列![]() 的任意連續三項均能構成一個三角形的三邊長,則稱
的任意連續三項均能構成一個三角形的三邊長,則稱![]() 為三角形”數列對于“三角形”數列
為三角形”數列對于“三角形”數列![]() ,如果函數
,如果函數![]() 使得
使得![]() 仍為一個三角形”數列,則稱
仍為一個三角形”數列,則稱![]() 是數列
是數列![]() 的“保三角形函數”
的“保三角形函數”![]() .
.
(1)已知![]() 是首項為2,公差為1的等差數列,若
是首項為2,公差為1的等差數列,若![]() ,
,![]() 是數列
是數列![]() 的保三角形函數”,求
的保三角形函數”,求![]() 的取值范圍;
的取值范圍;
(2)已知數列![]() 的首項為2019,
的首項為2019,![]() 是數列
是數列![]() 的前
的前![]() 項和,且滿足
項和,且滿足![]() ,證明
,證明![]() 是“三角形”數列;
是“三角形”數列;
(3)求證:函數![]() ,
,![]() 是數列1,
是數列1,![]() ,
,![]() 的“保三角形函數”的充要條件是
的“保三角形函數”的充要條件是![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com