【題目】在平面直角坐標系xOy中，直線l的參數方程為
（t為參數），若以O為極點，x軸的正半軸為極軸且取相同的單位長度建立極坐標系，曲線C的極坐標方程為
.
（1）求曲線C的直角坐標方程及直線l的普通方程；
（2）將所得曲線C向右平移1個單位長度，再將曲線C上的所有點的橫坐標變為原來的2倍，得到曲線
，求曲線上的點到直線l的距離的最大值.
科目：高中數學 來源： 題型：
【題目】已知直線
與直線
互相垂直，且交點為Q，點
，線段QF的垂直平分線與直線交于點P．
（I）若動點P的軌跡為曲線E，求曲線E的方程；
（Ⅱ）已知點
，經過點M的兩條直線分別與曲線E交于A，B和C，D，且
，設直線AC，BD的斜率分別為
，是否存在常數
，使得當
變動時，
？說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝log3（ax+b）的圖象經過點A（2，1）和B（5，2），an＝an+b（n∈N*）．
（1）求{an}；
（2）設數列{an}的前n項和為Sn，bn
，求{bn}的前n項和Tn．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
，
，
，
，過點
作平面
的垂線，垂足為
與
的交點
，
是線段
的中點.
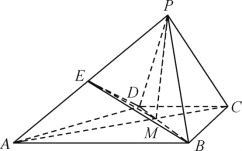
（1）求證：DE//平面
；
（2）若四棱錐的體積為
，求直線
與平面所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著城市化、工業化進程加速，汽車工業快速發展，國際原油供求矛盾逐步加深，全球氣候變暖日益明顯.在此背景下，以節能減排為重要目標的新能源汽車技術不斷取得突破，并呈現快速突破、競相發展的態勢.在2015年10月份，國家發改委等部委在《電動汽車充電基礎設施發展指南（2015-2020年）》中要求，新建住宅配建停車位應100%建設充電基礎設施或預留建設安裝條件，大型公共建筑物配建停車場、社會公共停車場建設充電基礎設施或預留建設安裝條件的車位比例不低于10%，每2000輛電動汽車應至少配套建設一座公共充電站.
為鼓勵新能源汽車發展，國家和地方出臺了相關補貼政策.
附表1：2018年某市新能源汽車補貼政策：
純電續航里程（ | 國家補貼（萬元/輛） | 地方補貼（萬元/輛） |
| 1.50 | 0.75 |
| 2.4 | 1.2 |
| 3.4 | 1.7 |
| 4.5 | 2.25 |
| 5 | 2.5 |
為了獲得更大的市場分額，搶占未來新能源汽車銷售先機.該市對2018年各類型新能源汽車銷售占比情況進行了調查.
附表2：2018年該市各類型新能源汽車銷售占比情況：
純電續航里程 |
|
|
|
|
|
占比 | 5% | 20% | 35% | 25% | 15% |
（1）用2018年新能源汽車銷售占比來估計2019年的新能源汽車銷售情況，求2019年每輛新能源汽車的平均補貼.若該市2019年想實現3000萬元補貼，估計需要銷售新能源汽車多少量.（補貼政策按每輛車補貼=國家補貼+地方補貼，結果四舍五入保留整數）
（2）該市新能源汽車促進辦公寶為了調查新能源汽車補貼發放情況，希望從2018年銷售的新能漂源汽車中抽取10輛車的信息進行回訪核實.以各類型新能源汽車銷售占比為概率.求抽到幾輛續航里程小于
新能源汽車的可能性最大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對數列
，規定
為數列的一階差分數列，其中
，規定
為的二階差分數列，其中
.
（1）數列的通項公式
，試判斷，是否為等差數列，請說明理由？
（2）數列
是公比為
的正項等比數列，且
，對于任意的
，都存在
，使得
，求所有可能的取值構成的集合；
（3）各項均為正數的數列
的前
項和為
，且
，對滿足
，
的任意正整數
、、
，都有
，且不等式
恒成立，求實數
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知有窮數列A：
（
且
）.定義數列A的“伴生數列”B：
，其中
（
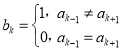），規定
，
.
（1）寫出下列數列的“伴生數列”：
①1，2，3，4，5；
②1，
，1，，1.
（2）已知數列B的“伴生數列”C：
，
，…，
，…，
，且滿足
（
，2，…，n）.
（i）若數列B中存在相鄰兩項為1，求證：數列B中的每一項均為1；
（ⅱ）求數列C所有項的和.
查看答案和解析>>
科目：高中數學 來源： 題型：
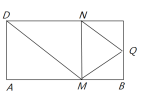
【題目】如圖,矩形
中,
,
,
為
的中點,點
,
分別在線段
,
上運動（其中不與
,
重合,不與
,
重合）,且
,沿
將
折起,得到三棱錐
,則三棱錐體積的最大值為__________；當三棱錐體積最大時,其外接球的表面積的值為_______________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列
（
）的各項均為正整數，且
.若對任意
，存在正整數
使得
，則稱數列
具有性質
.
（1）判斷數列
與數列
是否具有性質；（只需寫出結論）
（2）若數列具有性質，且
，
，
，求
的最小值；
（3）若集合
，且
（任意
，
）.求證：存在
，使得從中可以選取若干元素（可重復選取）組成一個具有性質的數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
