
【題目】已知函數(shù)![]() (常數(shù)
(常數(shù)![]() ).
).
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)![]() 是
是![]() 的導(dǎo)函數(shù),求證:
的導(dǎo)函數(shù),求證:![]() .
.
【答案】(1)見解析;(2)見解析.
【解析】試題分析:(1)先求導(dǎo)數(shù),再求導(dǎo)函數(shù)零點(diǎn),根據(jù)兩零點(diǎn)大小分類討論,確定導(dǎo)函數(shù)符號變化規(guī)律,進(jìn)而確定單調(diào)性,(2)先化簡所證不等式,再利用導(dǎo)函數(shù)證![]() (
(![]() ),即得
),即得![]() (
(![]() ),最后再利用導(dǎo)數(shù)證
),最后再利用導(dǎo)數(shù)證![]() (差函數(shù)或商函數(shù)),根據(jù)
(差函數(shù)或商函數(shù)),根據(jù)
等號不同時成立得結(jié)論.
試題解析:(1)![]() (
(![]() ,
,![]() )
)
畫出![]() (
(![]() )及
)及![]() (
(![]() )的圖象,它們的零點(diǎn)分別為
)的圖象,它們的零點(diǎn)分別為![]() 和
和![]()
①當(dāng)![]() 時,
時,![]() 在
在![]()
![]() ,
,![]() ,
,![]()
②當(dāng)![]() 時,
時,![]() 在
在![]()
③當(dāng)![]() 時,
時,![]() 在
在![]() ,
,![]() ,
,![]()
(2)因![]()
要證![]() ,需證
,需證![]() (
(![]() )
)
法1.即證![]() (
(![]() )
)
設(shè)![]() (
(![]() ),
),![]() (
(![]() )
)
一方面![]() (
(![]() )
)![]() 在
在![]() ,
,![]()
則![]() ①
①
另一方面,![]() (
(![]() )
)![]() 在
在![]() ,
,![]()
則![]() ②
②
據(jù)①②![]()
有因①的取等條件是![]() ,②的取等條件是
,②的取等條件是![]()
故![]() ,即
,即![]() (
(![]() ),即
),即![]()
法2先證![]() (
(![]() )(差函數(shù))
)(差函數(shù))
進(jìn)而![]() (
(![]() )
)
再證![]() (差函數(shù)或商函數(shù))
(差函數(shù)或商函數(shù))
說明等號不成立
故![]() (
(![]() )成立.
)成立.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一只紅鈴蟲的產(chǎn)卵數(shù)y和溫度x有關(guān),現(xiàn)收集了6組觀測數(shù)據(jù)于下表中,通過散點(diǎn)圖可以看出樣本點(diǎn)分布在一條指數(shù)型函數(shù)y=![]() 的圖象的周圍.
的圖象的周圍.
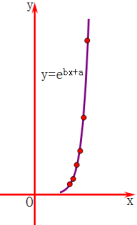
(1)試求出y關(guān)于x的上述指數(shù)型的回歸曲線方程(結(jié)果保留兩位小數(shù));
(2)試用(1)中的回歸曲線方程求相應(yīng)于點(diǎn)(24,17)的殘差![]() .(結(jié)果保留兩位小數(shù))
.(結(jié)果保留兩位小數(shù))
溫度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
產(chǎn)卵數(shù)y(個) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
幾點(diǎn)說明:
①結(jié)果中的![]() 都應(yīng)按題目要求保留兩位小數(shù).但在求
都應(yīng)按題目要求保留兩位小數(shù).但在求![]() 時請將
時請將![]() 的值多保留一位即用保留三位小數(shù)的結(jié)果代入.
的值多保留一位即用保留三位小數(shù)的結(jié)果代入.
②計(jì)算過程中可能會用到下面的公式:回歸直線方程的斜率![]() =
= =
= ,截距
,截距![]() .
.
③下面的參考數(shù)據(jù)可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某興趣小組進(jìn)行“野島生存”實(shí)踐活動,他們設(shè)置了![]() 個取水敞口箱.其中
個取水敞口箱.其中![]() 個采用
個采用![]() 種取水法,
種取水法,![]() 個采用
個采用![]() 種取水法.如圖甲為
種取水法.如圖甲為![]() 種方法一個夜晚操作一次
種方法一個夜晚操作一次![]() 個水箱積取淡水量頻率分布直方圖,圖乙為
個水箱積取淡水量頻率分布直方圖,圖乙為![]() 種方法一個夜晚操作一次
種方法一個夜晚操作一次![]() 個水箱積取淡水量頻率分布直方圖.
個水箱積取淡水量頻率分布直方圖.
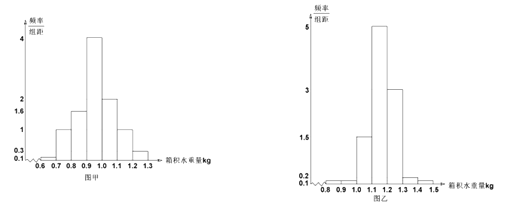
(1)設(shè)兩種取水方法互不影響,設(shè)![]() 表示事件“
表示事件“![]() 法取水箱水量不低于
法取水箱水量不低于![]() ,
,![]() 法取水箱水量不低于
法取水箱水量不低于![]() ”,以樣本估計(jì)總體,以頻率分布直方圖中的頻率為概率,估計(jì)
”,以樣本估計(jì)總體,以頻率分布直方圖中的頻率為概率,估計(jì)![]() 的概率;
的概率;
(2)填寫下面![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 的把握認(rèn)為箱積水量與取水方法有關(guān).
的把握認(rèn)為箱積水量與取水方法有關(guān).
箱積水量 | 箱積水量 | 箱數(shù)總計(jì) | |
| |||
| |||
箱數(shù)總計(jì) |
附:![]()
![]()

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為凈化新安江水域的水質(zhì),市環(huán)保局于2017年底在新安江水域投入一些蒲草,這些蒲草在水中的蔓延速度越來越快,2018年二月底測得蒲草覆蓋面積為![]() ,2018年三月底測得覆蓋面積為
,2018年三月底測得覆蓋面積為![]() ,蒲草覆蓋面積
,蒲草覆蓋面積![]() (單位:
(單位:![]() )與月份
)與月份![]() (單位:月)的關(guān)系有兩個函數(shù)模型
(單位:月)的關(guān)系有兩個函數(shù)模型![]() 與
與![]() 可供選擇.
可供選擇.
(Ⅰ)分別求出兩個函數(shù)模型的解析式;
(Ⅱ)若市環(huán)保局在2017年年底投放了![]() 的蒲草,試判斷哪個函數(shù)模型更合適?并說明理由;
的蒲草,試判斷哪個函數(shù)模型更合適?并說明理由;
(Ⅲ)利用(Ⅱ)的結(jié)論,求蒲草覆蓋面積達(dá)到![]() 的最小月份.
的最小月份.
(參考數(shù)據(jù):![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為2的正方形ABCD中,E為線段AB的中點(diǎn),將△ADE沿直線DE翻折成△A′DE,使得平面A′DE⊥平面BCDE,F為線段A′C的中點(diǎn).
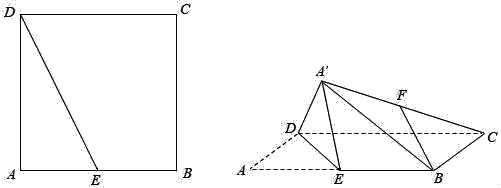
(Ⅰ)求證:BF∥平面A′DE;
(Ⅱ)求直線A′B與平面A′DE所成角的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正三棱柱![]() 各條棱的長度均相等,
各條棱的長度均相等,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 分別是線段
分別是線段![]() 和線段
和線段![]() 上的動點(diǎn)(含端點(diǎn)),且滿足
上的動點(diǎn)(含端點(diǎn)),且滿足![]() ,當(dāng)
,當(dāng)![]() 運(yùn)動時,下列結(jié)論中不正確的是( )
運(yùn)動時,下列結(jié)論中不正確的是( )

A. 在![]() 內(nèi)總存在與平面
內(nèi)總存在與平面![]() 平行的線段
平行的線段
B. 平面![]() 平面
平面![]()
C. 三棱錐![]() 的體積為定值
的體積為定值
D. ![]() 可能為直角三角形
可能為直角三角形
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)等差數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,下列說法錯誤的是( )
,下列說法錯誤的是( )
A. 若![]() 有最大值,則
有最大值,則![]() 也有最大值
也有最大值
B. 若![]() 有最大值,則
有最大值,則![]() 也有最大值
也有最大值
C. 若數(shù)列![]() 不單調(diào),則數(shù)列
不單調(diào),則數(shù)列![]() 也不單調(diào)
也不單調(diào)
D. 若數(shù)列![]() 不單調(diào),則數(shù)列
不單調(diào),則數(shù)列![]() 也不單調(diào)
也不單調(diào)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了讓學(xué)生了解環(huán)保知識,增強(qiáng)環(huán)保意識,某中學(xué)舉行了一次“環(huán)保知識競賽”,共有900名學(xué)生參加了這次競賽. 為了解本次競賽成績情況,從中抽取了部分學(xué)生的成績(得分均為整數(shù),滿分為100分)進(jìn)行統(tǒng)計(jì). 請你根據(jù)尚未完成并有局部污損的頻率分布表和頻數(shù)分布直方圖,解答下列問題:


(1)填充頻率分布表的空格(將答案直接填在表格內(nèi));
(2)補(bǔ)全頻數(shù)分布直方圖;
(3)若成績在75.585.5分的學(xué)生為二等獎,問獲得二等獎的學(xué)生約為多少人?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() 是定義域?yàn)?/span>
是定義域?yàn)?/span>![]() 的偶函數(shù),當(dāng)
的偶函數(shù),當(dāng)![]() 時,
時, ,若關(guān)于
,若關(guān)于![]() 的方程
的方程![]() ,
,![]() ,有且僅有5個不同實(shí)數(shù)根,則實(shí)數(shù)a的取值范圍是______.
,有且僅有5個不同實(shí)數(shù)根,則實(shí)數(shù)a的取值范圍是______.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com