
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,四邊形ABCD為正方形,AB=PA=4,A點在PD上的射影為G點,E點在AB上,平面PCE⊥平面PCD. 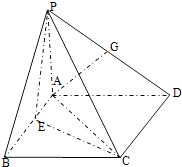
(1)求證:AG⊥平面PCD;
(2)求直線PD與平面PCE所成角的正弦值.
【答案】
(1)證明:∵CD⊥AD,CD⊥PA,AD∩PA=A
∴CD⊥平面PAD∴CD⊥AG,
又PD⊥AG,CD∩PD=D
∴AG⊥平面PCD
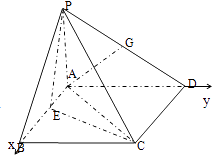
(2)解:如圖建立坐標系,則P(0,0,3),C(4,4,0),D(0,4,0),G(0,2,2),
設E(a,0,0),由(1)知: ![]() 是面PCD的法向量,
是面PCD的法向量,
又 ![]() ,
, ![]() ,設面PCE的法向量為
,設面PCE的法向量為 ![]() ,
,
則 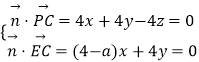 ,取x=4,得:
,取x=4,得: ![]()
因平面PCE⊥平面PCD, ![]() ,∴a=2,即:
,∴a=2,即: ![]()
又 ![]() ,設PD與面PCE所成的角為θ,
,設PD與面PCE所成的角為θ,
則: 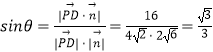
【解析】(1)先證明出CD⊥平面PAD,進而可推斷出CD⊥AG,然后利用AG⊥PD,根據線面垂直的判定定理證明出結論.(2)建立坐標系,先求出面PCE的法向量,再利用向量的夾角公式求出直線PD與平面PCE所成角的正弦值.
【考點精析】根據題目的已知條件,利用直線與平面垂直的判定和空間角的異面直線所成的角的相關知識可以得到問題的答案,需要掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則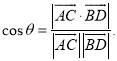 .
.


科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A、B、C所對的邊分別是a、b、c,且a+b+c=8.
(1)若a=2,b= ![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2 ![]() +sinBcos2
+sinBcos2 ![]() =2sinC,且△ABC的面積S=
=2sinC,且△ABC的面積S= ![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
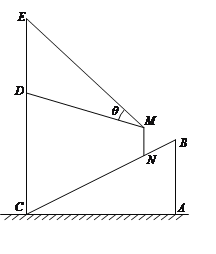
【題目】某商場在一部向下運行的手扶電梯終點的正上方豎直懸掛一幅廣告畫.如圖,該電梯的高![]() 為
為![]() 米,它所占水平地面的長
米,它所占水平地面的長![]() 為
為![]() 米.該廣告畫最高點
米.該廣告畫最高點![]() 到地面的距離為
到地面的距離為![]() 米,最低點
米,最低點![]() 到地面距離
到地面距離![]() 米.假設某人眼睛到腳底的距離
米.假設某人眼睛到腳底的距離![]() 為
為![]() 米,他豎直站在此電梯上觀看
米,他豎直站在此電梯上觀看![]() 視角為
視角為![]() .
.
(Ⅰ)設此人到直線![]() 的距離為
的距離為![]() 米,試用含
米,試用含![]() 的表達式表示
的表達式表示![]() ;
;
(Ⅱ)此人到直線![]() 的距離為多少米時,視角
的距離為多少米時,視角![]() 最大?
最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某投資公司計劃投資A,B兩種金融產品,根據市場調查與預測,A產品的利潤y1與投資金額x的函數關系為y1=18﹣ ![]() ,B產品的利潤y2與投資金額x的函數關系為y2=
,B產品的利潤y2與投資金額x的函數關系為y2= ![]() (注:利潤與投資金額單位:萬元).
(注:利潤與投資金額單位:萬元).
(1)該公司已有100萬元資金,并全部投入A,B兩種產品中,其中x萬元資金投入A產品,試把A,B兩種產品利潤總和表示為x的函數,并寫出定義域;
(2)在(1)的條件下,試問:怎樣分配這100萬元資金,才能使公司獲得最大利潤?其最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=Asin(ωx+φ)在一個周期內的圖象如圖,此函數的解析式為( ) 
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
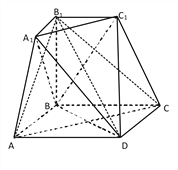
【題目】如圖所示的幾何體是由棱臺![]() 和棱錐
和棱錐![]() 拼接而成的組合體,其底面四邊形
拼接而成的組合體,其底面四邊形![]() 是邊長為
是邊長為![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求證:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣e﹣x+4sin3x+1,x∈(﹣1,1),若f(1﹣a)+f(1﹣a2)>2成立,則實數a的取值范圍是( )
A.(﹣2,1)
B.(0,1)
C.![]()
D.(﹣∞,﹣2)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() cos4x+2sinxcosx﹣
cos4x+2sinxcosx﹣ ![]() sin4x.
sin4x.
(1)當x∈[0, ![]() ]時,求f(x)的最大值、最小值以及取得最值時的x值;
]時,求f(x)的最大值、最小值以及取得最值時的x值;
(2)設g(x)=3﹣2m+mcos(2x﹣ ![]() )(m>0),若對于任意x1∈[0,
)(m>0),若對于任意x1∈[0, ![]() ],都存在x2∈[0,
],都存在x2∈[0, ![]() ],使得f(x1)=g(x2)成立,求實數m的取值范圍.
],使得f(x1)=g(x2)成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com