
【題目】已知函數f(x)= ![]() (a>0,且a≠1)在R上單調遞減,且關于x的方程|f(x)|=2﹣x恰好有兩個不相等的實數解,則a的取值范圍是( )
(a>0,且a≠1)在R上單調遞減,且關于x的方程|f(x)|=2﹣x恰好有兩個不相等的實數解,則a的取值范圍是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
【答案】C
【解析】解:y=loga(x+1)+1在[0,+∞)遞減,則0<a<1, 函數f(x)在R上單調遞減,則: ;
;
解得, ![]() ;
;
由圖象可知,在[0,+∞)上,|f(x)|=2﹣x有且僅有一個解,
故在(﹣∞,0)上,|f(x)|=2﹣x同樣有且僅有一個解,
當3a>2即a> ![]() 時,聯立|x2+(4a﹣3)x+3a|=2﹣x,
時,聯立|x2+(4a﹣3)x+3a|=2﹣x,
則△=(4a﹣2)2﹣4(3a﹣2)=0,
解得a= ![]() 或1(舍去),
或1(舍去),
當1≤3a≤2時,由圖象可知,符合條件,
綜上:a的取值范圍為[ ![]() ,
, ![]() ]∪{
]∪{ ![]() },
},
故選:C.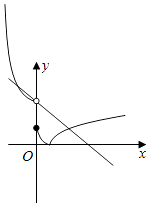
利用函數是減函數,根據對數的圖象和性質判斷出a的大致范圍,再根據f(x)為減函數,得到不等式組,利用函數的圖象,方程的解的個數,推出a的范圍.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】兩條平行直線和圓的位置關系定義為:若兩條平行直線和圓有四個不同的公共點,則稱兩條平行線和圓“相交”;若兩平行直線和圓沒有公共點,則稱兩條平行線和圓“相離”;若兩平行直線和圓有一個、兩個或三個不同的公共點,則稱兩條平行線和圓“相切”.已知直線![]() ,
,![]() ,和圓:
,和圓:![]() 相切,則實數
相切,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() 或
或![]() B.
B. ![]() 或
或![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,已知a1>1,an+1=an2﹣an+1(n∈N*),且 ![]()
![]() +…+
+…+ ![]() =2.則當a2016﹣4a1取得最小值時,a1的值為= .
=2.則當a2016﹣4a1取得最小值時,a1的值為= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市地產數據研究所的數據顯示,2016年該市新建住宅銷售均價走勢如圖所示,3月至7月房價上漲過快,政府從8月采取宏觀調控措施,10月份開始房價得到很好的抑制.

(1)地產數據研究所發現,3月至7月的各月均價![]() (萬元/平方米)與月份
(萬元/平方米)與月份![]() 之間具有較強的線性相關關系,試求
之間具有較強的線性相關關系,試求![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
(2)若政府不調控,按照3月份至7月份房價的變化趨勢預測12月份該市新建住宅的銷售均價.
參考數據:![]() ,
,![]() ,
,![]() ;
;
參考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某輪胎集團有限公司生產的輪胎的寬度![]() (單位:
(單位: ![]() )服從正態分布
)服從正態分布![]() ,公司規定:輪胎寬度不在
,公司規定:輪胎寬度不在![]() 內將被退回生產部重新生產.
內將被退回生產部重新生產.
(1)求此輪胎不被退回的概率(結果精確到![]() );
);
(2)現在該公司有一批輪胎需要進行初步質檢,檢驗方案是從這批輪胎中任取![]() 件作檢驗,這
件作檢驗,這![]() 件產品中至少有
件產品中至少有![]() 件不被退回生產部,則稱這批輪胎初步質檢合格.
件不被退回生產部,則稱這批輪胎初步質檢合格.
()求這批輪胎初步質檢合格的概率;
()若質檢部連續質檢了![]() 批輪胎,記
批輪胎,記![]() 為這
為這![]() 批輪胎中初步質檢合格的批數,求
批輪胎中初步質檢合格的批數,求![]() 的數學期望.
的數學期望.
附:若![]() ,則
,則![]()
![]()
![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列{an}的前n項和為Sn , 且4Sn=(an+1)2(n∈N+). (Ⅰ)求數列{an}的通項公式;
(Ⅱ)設Tn為數列{ ![]() }的前n項和,證明:
}的前n項和,證明: ![]() ≤Tn<1(n∈N+).
≤Tn<1(n∈N+).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型商場為了了解顧客的購物信息,隨機在商場收集了![]() 位顧客的購物總額(單位元),將數據按照
位顧客的購物總額(單位元),將數據按照![]()
![]() ,
,![]()
![]() 分成
分成![]() 組,制成了如下圖所示的頻率分布直方圖:
組,制成了如下圖所示的頻率分布直方圖:
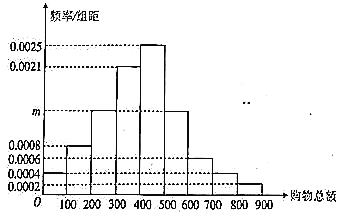
該商場每日大約有![]() 名顧客,為了增加商場銷售總額,近期對一次性購物不低于
名顧客,為了增加商場銷售總額,近期對一次性購物不低于![]() 元的顧客發放紀念品.
元的顧客發放紀念品.
(1)求頻率分布直方圖中![]() 的值,并估計每日應準備紀念品的數量;
的值,并估計每日應準備紀念品的數量;
(2)若每日按分層抽樣的方法從購物總額在![]() 三組對應的顧客中抽取
三組對應的顧客中抽取![]() 名顧客,這
名顧客,這![]() 名顧客中再隨機抽取兩名超級顧客,每人獎勵一個超級禮包,求獲得超級禮包的兩人來自不同組的概率.
名顧客中再隨機抽取兩名超級顧客,每人獎勵一個超級禮包,求獲得超級禮包的兩人來自不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]()

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱錐P-ABCD的體積為
,且四棱錐P-ABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com