
給出下列4個(gè)命題:①若 ,則
,則 是等腰三角形;②若
是等腰三角形;②若 ,則
,則 是直角三角形;③若
是直角三角形;③若 ,則
,則 是鈍角三角形;④若
是鈍角三角形;④若 ,則
,則 是等邊三角形.其中正確的命題是( )
是等邊三角形.其中正確的命題是( )
| A.①③ | B.③④ | C.①④ | D.②③ |
B
解析試題分析:①若sin2A=sin2B,則 2A=2B,或 2A+2B=π,即A="B" 或C=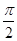 ,故△ABC為等腰三角形 或直角三角形,故①不正確.
,故△ABC為等腰三角形 或直角三角形,故①不正確.
②若sinA=cosB,不能推出△ABC是直角三角形,如A=B=45°時(shí),雖有sinA=cosB,但△ABC不是直角三角形,故②不正確.
③若cosA•cosB•cosC<0,則由三角形各個(gè)內(nèi)角的范圍及內(nèi)角和等于180° 知,cosA、cosB、cosC兩個(gè)是正實(shí)數(shù),一個(gè)是負(fù)數(shù),故A、B、C中兩個(gè)是銳角,一個(gè)是鈍角,故③正確.
④若cos(A-B)•cos(B-C)•cos(C-A)=1,則由三角形各個(gè)內(nèi)角的范圍及內(nèi)角和等于180° 知,
cos(A-B)=cos(B-C)=cos(C-A)=1,故有 A=B=C,故△ABC是等邊三角形,故④正確.
即③④正確,故選B.
考點(diǎn):和差的三角函數(shù)公式,三角形的特征。
點(diǎn)評(píng):典型題,本題較綜合的考察三角形的基本特征以及和差的三角函數(shù)公式,屬于中檔題。


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:單選題
給出下列三個(gè)結(jié)論:
①命題“若
 ,則方程
,則方程
 有實(shí)數(shù)根”的逆否命題為:“若方程
有實(shí)數(shù)根”的逆否命題為:“若方程
 無實(shí)數(shù),則
無實(shí)數(shù),則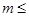 0”.
0”.
②若
 為假命題,則p,q均為假命題.
為假命題,則p,q均為假命題.
③若命題
 ,則
,則
 .
.
其中正確結(jié)論的個(gè)數(shù)為
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
已知a,b是實(shí)數(shù),則“| a+b |=| a |+| b |”是“ab>0”的
| A.充分不必要條件 | B.必要不充分條件 |
| C.充分必要條件 | D.既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
“三角形有一個(gè)內(nèi)角為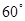 ”是“三內(nèi)角成等差數(shù)列”的( )
”是“三內(nèi)角成等差數(shù)列”的( )
| A.充分不必要條件 | B.必要不充分條件 |
| C.充要條件 | D.既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
設(shè)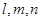 均為直線,其中
均為直線,其中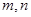 在平面
在平面 內(nèi),則
內(nèi),則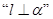 是
是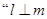 且
且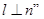 的
的
| A.充分不必要條件 | B.必要不充分條件 |
| C.充分必要條件 | D.既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
下面是關(guān)于復(fù)數(shù) 的三個(gè)命題:
的三個(gè)命題: 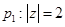
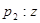 在復(fù)平面內(nèi)對(duì)應(yīng)的點(diǎn)在第四象限
在復(fù)平面內(nèi)對(duì)應(yīng)的點(diǎn)在第四象限 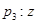 是純虛數(shù)
是純虛數(shù)
其中的真命題為
A.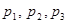 | B.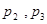 | C.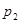 | D.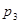 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com