
【題目】設函數(shù)f(x)=x2ex
(1)求f(x)的單調區(qū)間;
(2)若x∈[﹣2,2]時,不等式f(x)<m恒成立,求m的取值范圍.
【答案】
(1)解:f′(x)=x(x+2)ex,
令f′(x)>0,解得:x<﹣2或x>0,
令f′(x)<0,解得:﹣2<x<0,
∴函數(shù)f(x)的單調遞增區(qū)間為(﹣∞,﹣2)和(0,+∞),遞減區(qū)間為[﹣2,0].
(2)解:
x | ﹣2 | (﹣2,0) | 0 | (0,2) | 2 |
f′(x) | 0 | + | |||
f(x) |
| 單減 | 極小值0 | 單增 | 4e2 |
因此x∈[﹣2,2],f(x)的最大值是4e2,
∵x∈[﹣2,2]時,不等式f(x)<m恒成立,
∴m>4e2
【解析】(1)先求出函數(shù)的導數(shù),通過解關于導函數(shù)的不等式,求出其單調區(qū)間即可;(2)先求出f(x)在[﹣1,2]上的單調性,從而求出函數(shù)的最大值,即可求m的取值范圍.
【考點精析】利用利用導數(shù)研究函數(shù)的單調性和函數(shù)的最大(小)值與導數(shù)對題目進行判斷即可得到答案,需要熟知一般的,函數(shù)的單調性與其導數(shù)的正負有如下關系: 在某個區(qū)間![]() 內,(1)如果
內,(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調遞增;(2)如果
在這個區(qū)間單調遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個區(qū)間單調遞減;求函數(shù)
在這個區(qū)間單調遞減;求函數(shù)![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數(shù)
上的最大值與最小值的步驟:(1)求函數(shù)![]() 在
在![]() 內的極值;(2)將函數(shù)
內的極值;(2)將函數(shù)![]() 的各極值與端點處的函數(shù)值
的各極值與端點處的函數(shù)值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


科目:高中數(shù)學 來源: 題型:
【題目】定義在![]() 上的偶函數(shù)
上的偶函數(shù)![]() ,其導函數(shù)為
,其導函數(shù)為![]() ,若對任意的實數(shù)
,若對任意的實數(shù)![]() ,都有
,都有![]() 恒成立,則使
恒成立,則使![]() 成立的實數(shù)
成立的實數(shù)![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B. (﹣∞,﹣1)∪(1,+∞)
B. (﹣∞,﹣1)∪(1,+∞)
C. (﹣1,1) D. (﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)試討論![]() 的單調性;
的單調性;
(2)證明:對于正數(shù)![]() ,存在正數(shù)
,存在正數(shù)![]() ,使得當
,使得當![]() 時,有
時,有![]() ;
;
(3)設(1)中的![]() 的最大值為
的最大值為![]() ,求
,求![]() 得最大值.
得最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】小王于年初用50萬元購買一輛大貨車,第一年因繳納各種費用需支出6萬元,從第二年起,每年都比上一年增加支出2萬元,假定該車每年的運輸收入均為25萬元.小王在該車運輸累計收入超過總支出后,考慮將大貨車作為二手車出售,若該車在第x年年底出售,其銷售價格為(25-x)萬元(國家規(guī)定大貨車的報廢年限為10年).
(1)大貨車運輸?shù)降趲啄昴甑祝撥囘\輸累計收入超過總支出?
(2)在第幾年年底將大貨車出售,能使小王獲得的年平均利潤最大?(利潤=累計收入+銷售收入-總支出)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)y=ax在區(qū)間[0,2]上的最大值和最小值的和為5,則函數(shù)y=logax在區(qū)間[ ![]() ,2]上的最大值和最小值之差是( )
,2]上的最大值和最小值之差是( )
A.1
B.3
C.4
D.5
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面
的底面![]() 是平行四邊形,側面
是平行四邊形,側面![]() 是邊長為2的正三角形,
是邊長為2的正三角形, ![]() ,
, ![]() .
.
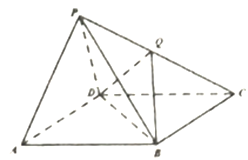
(1)求證:平面![]() 平面
平面![]() ;
;
(2)設![]() 是棱
是棱![]() 上的點,當
上的點,當![]() 平面
平面![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在10件產(chǎn)品中,有2件一等品,4件二等品,4件三等品,從這10件產(chǎn)品中任取3件,求
(1)取出的3件產(chǎn)品中一等品件數(shù)X的分布列和數(shù)學期望;
(2)取出的3件產(chǎn)品中至多有1件一等品的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)f(x)= ![]() ﹣
﹣ ![]()
(1)證明函數(shù)f(x)是奇函數(shù);
(2)證明函數(shù)f(x)在(﹣∞,+∞)內是增函數(shù);
(3)求函數(shù)f(x)在[1,2]上的值域.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上且以3為周期的奇函數(shù),當
上且以3為周期的奇函數(shù),當![]() 時,
時, ![]() ,則函數(shù)
,則函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的零點個數(shù)是( )
上的零點個數(shù)是( )
A. 3 B. 5 C. 7 D. 9
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com