
【題目】為考查某種藥物預防疾病的效果,隨機抽查了50只服用藥的動物和50只未服用藥的動得知服用藥的動物中患病的比例是![]() ,未服用藥的動物中患病的比例為
,未服用藥的動物中患病的比例為![]() .
.
(I)根據以上數據完成下列2×2列聯表:
患病 | 未患病 | 總計 | |
服用藥 | |||
沒服用藥 | |||
總計 |
(II)能否有99%的把握認為藥物有效?并說明理由.
附:
| … | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| … | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |

 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)若![]() 在
在![]() 上存在極值點,求a的取值范圍;
上存在極值點,求a的取值范圍;
(2)設![]() ,
,![]() ,若
,若![]() 存在最大值,記為
存在最大值,記為![]() ,則當
,則當![]() 時,
時,![]() 是否存在最大值?若存在,求出其最大值;若不存在,請說明理由
是否存在最大值?若存在,求出其最大值;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】勒洛三角形是具有類似圓的“定寬性”的面積最小的曲線,它由德國機械工程專家,機構運動學家勒洛首先發現,其作法是:以等邊三角形每個頂點為圓心,以邊長為半徑,在另兩個頂點間作一段弧,三段弧圍成的曲邊三角形就是勒洛三角形,現在勒洛三角形中隨機取一點,則此點取自正三角形外的概率為( )
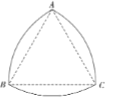
A.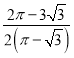 B.
B.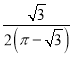
C.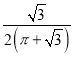 D.
D.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調研機構,對本地![]() 歲的人群隨機抽取
歲的人群隨機抽取![]() 人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,結果顯示,有
人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,結果顯示,有![]() 人為“低碳族”,該
人為“低碳族”,該![]() 人的年齡情況對應的頻率分布直方圖如圖.
人的年齡情況對應的頻率分布直方圖如圖.

(1)根據頻率分布直方圖,估計這![]() 名“低碳族”年齡的平均值,中位數;
名“低碳族”年齡的平均值,中位數;
(2)若在“低碳族”且年齡在![]() 、
、![]() 的兩組人群中,用分層抽樣的方法抽取
的兩組人群中,用分層抽樣的方法抽取![]() 人,試估算每個年齡段應各抽取多少人?
人,試估算每個年齡段應各抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,若點A為函數
,若點A為函數![]() 上的任意一點,點B為函數
上的任意一點,點B為函數![]() 上的任意一點.
上的任意一點.
(1)求A,B兩點之間距離的最小值;
(2)若A,B為函數![]() 與函數
與函數![]() 公切線的兩個切點,求證:這樣的點B有且僅有兩個,且滿足條件的兩個點B的橫坐標互為倒數.
公切線的兩個切點,求證:這樣的點B有且僅有兩個,且滿足條件的兩個點B的橫坐標互為倒數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量結果得如下頻數分布表:
質量指標值分組 |
|
|
|
|
|
頻數 | 6 | 26 | 38 | 22 | 8 |
(1)在答題卡上畫出這些數據的頻率分布直方圖(要求用陰影部分顯示);
(2)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“質量指標值不低于95的產品至少要占全部產品80%”的規定?
(3)估計這種產品質量指標值的平均值及中位數(其中求平均值時同一組中的數據用該組區間的中點值作代表,求中位數精確到0.1).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“韓信點兵”問題在我國古代數學史上有不少有趣的名稱,如“物不知數”“鬼谷算”“隔墻算”“大衍求一術”等,其中《孫子算經》中“物不知數”問題的解法直至1852年傳由傳教士傳入至歐洲,后驗證符合由高斯得出的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”. 原文如下:“今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二,問物幾何?”這是一個已知某數被3除余2,被5除余3,被7除余2,求此數的問題.現將1至2017這2017個數中滿足條件的數按由小到大的順序排成一列數,則中位數為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.平行的兩條直線的斜率一定存在且相等
B.平行的兩條直線的傾斜角一定相等
C.垂直的兩條直線的斜率之積為一1
D.只有斜率都存在且相等的兩條直線才平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人民生活水平的日益提高,某小區居民擁有私家車的數量與日俱增.由于該小區建成時間較早,沒有配套建造地下停車場,小區內無序停放的車輛造成了交通的擁堵.該小區的物業公司統計了近五年小區登記在冊的私家車數量(累計值,如147表示2016年小區登記在冊的所有車輛數,其余意義相同),得到如下數據:
編號 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
數量 | 37 | 104 | 147 | 196 | 216 |
(1)若私家車的數量![]() 與年份編號
與年份編號![]() 滿足線性相關關系,求
滿足線性相關關系,求![]() 關于
關于![]() 的線性回歸方程,并預測2020年該小區的私家車數量;
的線性回歸方程,并預測2020年該小區的私家車數量;
(2)小區于2018年底完成了基礎設施改造,劃設了120個停車位.為解決小區車輛亂停亂放的問題,加強小區管理,物業公司決定禁止無車位的車輛進入小區.由于車位有限,物業公司決定在2019年度采用網絡競拍的方式將車位對業主出租,租期一年,競拍方案如下:①截至2018年己登記在冊的私家車業主擁有競拍資格;②每車至多中請一個車位,由車主在競拍網站上提出申請并給出自己的報價;③根據物價部門的規定,競價不得超過1200元;④申請階段截止后,將所有申請的業主報價自高到低排列,排在前120位的業主以其報價成交;⑤若最后出現并列的報價,則以提出申請的時間在前的業主成交,為預測本次競拍的成交最低價,物業公司隨機抽取了有競拍資格的40位業主,進行了競拍意向的調查,并對他們的擬報競價進行了統計,得到如圖頻率分布直方圖:
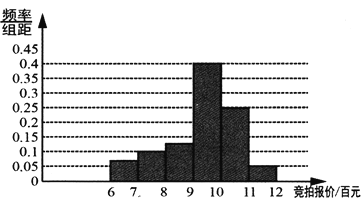
(i)求所抽取的業主中有意向競拍報價不低于1000元的人數;
(ii)如果所有符合條件的車主均參與競拍,利用樣本估計總體的思想,請你據此預測至少需要報價多少元才能競拍車位成功?(精確到整數)
參考公式及數據:對于一組數據![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: ;
;![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com