
【題目】已知函數![]() .
.
(1)若關于x的方程![]() 僅有1個實數根,求實數
僅有1個實數根,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() 是函數
是函數![]() 的極大值點,求實數a的取值范圍.
的極大值點,求實數a的取值范圍.
科目:高中數學 來源: 題型:
【題目】已知集合![]() ,集合
,集合![]() ,集合
,集合![]() .
.
(1)用列舉法表示集合C;
(2)設集合C的含n個元素所有子集為![]() ,記有限集合M的所有元素和為
,記有限集合M的所有元素和為![]() ,求
,求![]()
![]() 的值;
的值;
(3)已知集合P、Q是集合C的兩個不同子集,若P不是Q的子集,且Q不是P的子集,求所有不同的有序集合對![]() 的個數
的個數![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠從今年一月起,若不改善生產環境,按生產現狀,每月收入為80萬元,同時將受到環保部門的處罰,第一個月罰4萬元,以后每月增加2萬元.如果從今年一月起投資500萬元添加回收凈化設備(改造設備時間不計),一方面可以改善環境,另一方面可以大大降低原料成本,據測算,添加回收凈化設備并投產后的前4個月中的累計生產凈收入g(n)是生產時間![]() 個月的二次函數
個月的二次函數![]() 是常數
是常數![]() ,且前3個月的累計生產凈收入可達309萬元,從第5個月開始,每個月的生產凈收入都與第4個月相同,同時,該廠不但不受處罰,而且還將得到環保部門的一次性獎勵120萬元.
,且前3個月的累計生產凈收入可達309萬元,從第5個月開始,每個月的生產凈收入都與第4個月相同,同時,該廠不但不受處罰,而且還將得到環保部門的一次性獎勵120萬元.
(1)求前6個月的累計生產凈收入g(6)的值;
(2)問經過多少個月,投資開始見效,即投資改造后的純收入多于不改造的純收入.
查看答案和解析>>
科目:高中數學 來源: 題型:
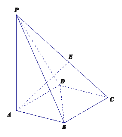
【題目】如圖,底面為正方形的四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() 為棱
為棱![]() 上一動點,
上一動點,![]() .
.
(1)當![]() 為
為![]() 中點時,求證:
中點時,求證:![]() 平面
平面![]() ;
;
(2)當![]() 平面
平面![]() 時,求
時,求![]() 的值;
的值;
(3)在(2)的條件下,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 、
、![]() 是三條不同的直線,
是三條不同的直線,![]() 、
、![]() 、
、![]() 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
②若![]() ,
,![]() ,則
,則![]() ;
;
③若![]() ,
,![]() 是兩條異面直線,
是兩條異面直線,![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() ,則
,則![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
其中正確命題的序號是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 經過橢圓
經過橢圓![]() :
: ![]() 的左右焦點
的左右焦點![]() ,且與橢圓
,且與橢圓![]() 在第一象限的交點為
在第一象限的交點為![]() ,且
,且![]() 三點共線,直線
三點共線,直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,且
兩點,且![]() (
(![]() ).
).
(1)求橢圓![]() 的方程;
的方程;
(2)當三角形![]() 的面積取得最大值時,求直線
的面積取得最大值時,求直線![]() 的方程.
的方程.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 中心在原點,焦點在坐標軸上,直線
中心在原點,焦點在坐標軸上,直線![]() 與橢圓
與橢圓![]() 在第一象限內的交點是
在第一象限內的交點是![]() ,點
,點![]() 在
在![]() 軸上的射影恰好是橢圓
軸上的射影恰好是橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 另一個焦點是
另一個焦點是![]() ,且
,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 過點
過點![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 的內切圓面積的最大值.
的內切圓面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
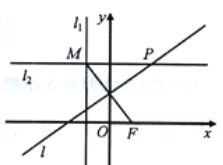
【題目】已知點![]() 和直線
和直線![]() ,直線
,直線![]() 過直線
過直線![]() 上的動點
上的動點![]() 且與直線
且與直線![]() 垂直,線段
垂直,線段![]() 的垂直平分線
的垂直平分線![]() 與直線
與直線![]() 相交于點
相交于點![]()
(I)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(II)設直線![]() 與軌跡
與軌跡![]() 相交于另一點
相交于另一點![]() ,與直線
,與直線![]() 相交于點
相交于點![]() ,求
,求![]() 的最小值
的最小值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com