
【題目】已知定義在(0, ![]() )上的函數(shù)f(x)的導(dǎo)函數(shù)為f′(x),且對于任意的x∈(0,
)上的函數(shù)f(x)的導(dǎo)函數(shù)為f′(x),且對于任意的x∈(0, ![]() ),都有f′(x)sinx<f(x)cosx,則( )
),都有f′(x)sinx<f(x)cosx,則( )
A.![]() f(
f( ![]() )>
)> ![]() f(
f( ![]() )
)
B.f( ![]() )>f(1)
)>f(1)
C.![]() f(
f( ![]() )<f(
)<f( ![]() )
)
D.![]() f(
f( ![]() )<f(
)<f( ![]() )
)
【答案】A
【解析】解:構(gòu)造函數(shù)g(x)= ![]() ,則f′(x)=
,則f′(x)= ![]() <0在x∈(0,
<0在x∈(0, ![]() )恒成立,
)恒成立,
∴g(x)在(0, ![]() )單調(diào)遞減,
)單調(diào)遞減,
∴g( ![]() )>g(
)>g( ![]() )>g(1)>g(
)>g(1)>g( ![]() ),
),
∴ ![]() >
> ![]() >
> ![]() >
> ![]() ,
,
∴ ![]() f(
f( ![]() )>f(
)>f( ![]() ),
), ![]() f(
f( ![]() )>f(
)>f( ![]() ),
), ![]() f(
f( ![]() )>
)> ![]() f(
f( ![]() ),sin
),sin ![]() f(1)>sin1f(
f(1)>sin1f( ![]() ),故無法比較f(
),故無法比較f( ![]() )與f(1)
)與f(1)
故選:A
【考點精析】解答此題的關(guān)鍵在于理解基本求導(dǎo)法則的相關(guān)知識,掌握若兩個函數(shù)可導(dǎo),則它們和、差、積、商必可導(dǎo);若兩個函數(shù)均不可導(dǎo),則它們的和、差、積、商不一定不可導(dǎo).


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)對于一切實數(shù)x,y均有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0,則當x∈(0, ![]() ),不等式f(x)+2<logax恒成立時,實數(shù)a的取值范圍是
),不等式f(x)+2<logax恒成立時,實數(shù)a的取值范圍是
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù), ![]() ),曲線
),曲線![]() 的參數(shù)方程為
的參數(shù)方程為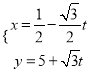 (
(![]() 為參數(shù)),以
為參數(shù)),以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立坐標系.
軸的正半軸為極軸建立坐標系.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)射線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以下是某地搜集到的新房屋的銷售價格![]() 和房屋的面積
和房屋的面積![]() 的數(shù)據(jù):
的數(shù)據(jù):
房屋面積( | 115 | 110 | 80 | 135 | 105 |
銷售價格(萬元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)畫出數(shù)據(jù)對應(yīng)的散點圖;
(2)求線性回歸方程,并在散點圖中加上回歸直線;
(3)據(jù)(2)的結(jié)果估計當房屋面積為150![]() 時的銷售價格.附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
時的銷售價格.附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
 ,
, ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,能推斷這個幾何體可能是三棱臺的是( ) 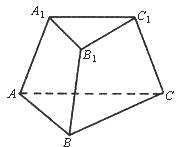
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1Bl=1,AB=2,BlCl=1.5,BC=3,A1C1=2,AC=3
C.AlBl=1,AB=2,B1Cl=1.5,BC=3,AlCl=2,AC=4
D.AB=A1B1 , BC=B1C1 , CA=C1A1
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
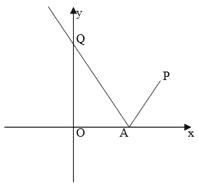
【題目】如圖,已知過點 ![]() 的光線,經(jīng)
的光線,經(jīng) ![]() 軸上一點
軸上一點 ![]() 反射后的射線
反射后的射線 ![]() 過點
過點 ![]() .
. 
(1)求點 ![]() 的坐標;
的坐標;
(2)若圓 ![]() 過點
過點 ![]() 且與
且與 ![]() 軸相切于點
軸相切于點 ![]() ,求圓
,求圓 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若圓C的半徑為1,圓心在第一象限,且與直線4x-3y=0和x軸都相切,則該圓的標準方程是( )
A.(x-2)2+(y-1)2=1
B.(x-2)2+(y-3)2=1
C.(x-3)2+(y-2)2=1
D.(x-3)2+(y-1)2=1
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com