【題目】已知
三個班共有學(xué)生100人，為調(diào)查他們的體育鍛煉情況，通過分層抽樣獲取了部分學(xué)生一周的鍛煉時間，數(shù)據(jù)如下表（單位：小時）.
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
（Ⅰ）試估計
班學(xué)生人數(shù)；
（Ⅱ）從
班和
班抽出來的學(xué)生中各選一名，記班選出的學(xué)生為甲，班選出的學(xué)生為乙，若學(xué)生鍛煉相互獨(dú)立，求甲的鍛煉時間大于乙的鍛煉時間的概率.
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在正三棱柱ABC-A1B1C1中，AB=AA1=2，點(diǎn)P，Q分別為A1B1，BC的中點(diǎn)．
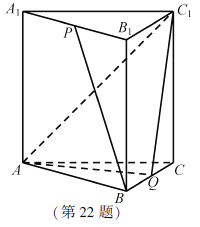
（1）求異面直線BP與AC1所成角的余弦值；
（2）求直線CC1與平面AQC1所成角的正弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】選修4-4：坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系
中，直線
的參數(shù)方程為
（
為參數(shù)）.以坐標(biāo)原點(diǎn)為極點(diǎn)，
軸的正半軸為極軸建立極坐標(biāo)系，已知曲線
的極坐標(biāo)方程為
.
（1）寫出直線的普通方程及曲線的直角坐標(biāo)方程；
（2）已知點(diǎn)
，點(diǎn)
，直線過點(diǎn)
且與曲線相交于
，
兩點(diǎn)，設(shè)線段
的中點(diǎn)為
，求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】一種藥在病人血液中的含量不低于2克時，它才能起到有效治療的作用．已知每服用m（
且
）個單位的藥劑，藥劑在血液中的含量y（克）隨著時間x（時）變化的函數(shù)關(guān)系式近似為
，其中
．
（1）若病人一次服用3個單位的藥劑，則有效治療時間可達(dá)多少小時？
（2）若病人第一次服用2個單位的藥劑，4個小時后再服用m個單位的藥劑，要使接下來的2個小時中能夠持續(xù)有效治療，試求m的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】給出下列四個命題：
① 函數(shù)
與函數(shù)
表示同一個函數(shù)．
② 奇函數(shù)的圖象一定過直角坐標(biāo)系的坐標(biāo)原點(diǎn)．
③ 函數(shù)
的圖象可由
的圖象向左平移
個單位長度得到．
④ 若函數(shù)
的定義域?yàn)?/span>
，則函數(shù)
的定義域?yàn)?/span>
．
其中正確命題的序號是_________ (填上所有正確命題的序號) ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知在四棱錐
中， 
為正三角形， 
，底面
為平行四邊形，平面
平面
，點(diǎn)
是側(cè)棱
的中點(diǎn)，平面
與棱
交于點(diǎn)
.
(1)求證： 
；
(2)若
，求平面
與平面
所成二面角（銳角）的余弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知在四棱錐
中，
平面
，點(diǎn)
在棱
上，且
，底面為直角梯形，
分別是
的中點(diǎn)．
（1）求證：
//平面
；
（2）求直線
與平面
所成角的正弦值；
（3）求點(diǎn)
到平面的距離.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在長方體
中，
，
，點(diǎn)
在棱
上移動．
（1）證明：
；
（2）求直線
與平面
所成的角；
（3）當(dāng)為的中點(diǎn)時，求三棱錐
的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
