本試題主要是考查了指數(shù)不等式的求解。現(xiàn)根據(jù)底數(shù)分情況討論,當
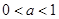
時,函數(shù)
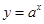
在
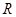
上為減函數(shù),由
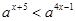
,得
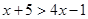
,即
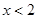
;當
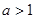
時,函數(shù)
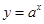
在
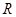
上為增函數(shù) 由
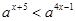
,得
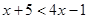
,即
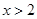
,綜上可知結論。
解:(1)當
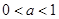
時,函數(shù)
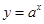
在
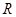
上為減函數(shù) ……………1分
由
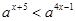
,得
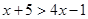
,即
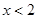
……………4分
(2)當
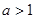
時,函數(shù)
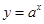
在
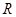
上為增函數(shù) ……………5分
由
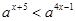
,得
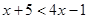
,即
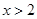
……………8分
綜上,當
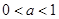
時,原不等式的解集為
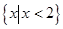
;當
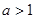
時,原不等式的解集為
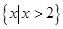
……………10分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
設
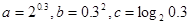
,則
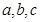
的大小關系是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
(1)化簡
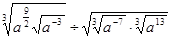
;
(2)已知
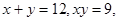
且
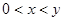
,求
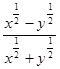
的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設
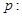
函數(shù)
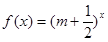
是增函數(shù),
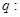
函數(shù)
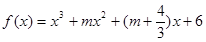
在R上有極值,求使命題“p且q”為真的實數(shù)m的取值范圍。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
當
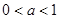
時,在同一坐標系中,函數(shù)
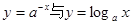
的圖象是( )
查看答案和解析>>

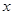 的不等式
的不等式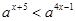 (
(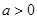 ,且
,且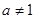 ).
).