
【題目】如圖,在四棱錐![]() 中,
中,![]() 是以
是以![]() 為斜邊的直角三角形,
為斜邊的直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)若線段![]() 上有一個點
上有一個點![]() ,使得
,使得![]() 平面
平面![]() ,請確定點
,請確定點![]() 的位置,并說明理由;
的位置,并說明理由;
(2)若平面![]() 平面
平面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)當P為AD的中點時,![]() 平面PBE(2)
平面PBE(2)![]()
【解析】
要證線面平行,需證明線線平行,所以取![]() 中點
中點![]() ,連接
,連接![]() ,即證明
,即證明![]() ;
;
(2)過B作![]() 于H,連結HE,證明
于H,連結HE,證明![]() 兩兩垂直,以點
兩兩垂直,以點![]() 為原點,建立空間直角坐標系,求平面
為原點,建立空間直角坐標系,求平面![]() 的法向量
的法向量![]() ,利用公式
,利用公式![]() 求解.
求解.
解:(1)當P為AD的中點時,![]() ,
,
又因為![]() 平面PBE,
平面PBE,![]() 平面PBE,所以
平面PBE,所以![]() 平面PBE.
平面PBE.
(2)過B作![]() 于H,連結HE,在等腰梯形ABCD中易知
于H,連結HE,在等腰梯形ABCD中易知![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,可得
,可得![]() .
.
又因為![]() ,平面
,平面![]() 平面ADE,
平面ADE,
且平面![]() 平面
平面![]() ,
,
所以![]() 平面ADE,所以
平面ADE,所以![]() .
.
如圖,以H為原點,HE,HD,HB所在直線分別為x軸,y軸,z軸建立空間直角坐標系.
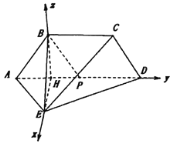
則![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.![]() .設平面ABE的一個法向量
.設平面ABE的一個法向量![]() ,
,
則![]() ,即
,即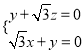 ,取
,取![]() ,得
,得![]() .
.
設直線CD與平面ABE所成角為![]() ,所以
,所以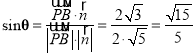 .
.


科目:高中數學 來源: 題型:
【題目】近年來,國資委.黨委高度重視扶貧開發工作,堅決貫徹落實中央扶貧工作重大決策部署,在各個貧困縣全力推進定點扶貧各項工作,取得了積極成效,某貧困縣為了響應國家精準扶貧的號召,特地承包了一塊土地,已知土地的使用面積以及相應的管理時間的關系如下表所示:
土地使用面積 | 1 | 2 | 3 | 4 | 5 |
管理時間 | 8 | 10 | 13 | 25 | 24 |
并調查了某村300名村民參與管理的意愿,得到的部分數據如下表所示:
愿意參與管理 | 不愿意參與管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相關系數![]() 的大小,并判斷管理時間
的大小,并判斷管理時間![]() 與土地使用面積
與土地使用面積![]() 是否線性相關?
是否線性相關?
(2)是否有99.9%的把握認為村民的性別與參與管理的意愿具有相關性?
(3)若以該村的村民的性別與參與管理意愿的情況估計貧困縣的情況,則從該貧困縣中任取3人,記取到不愿意參與管理的男性村民的人數為![]() ,求
,求![]() 的分布列及數學期望。
的分布列及數學期望。
參考公式:

![]()
其中![]() 。臨界值表:
。臨界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
參考數據:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】作為加班拍檔、創業伴侶、春運神器,曾幾何時,方便面是我們生活中重要的“朋友”,然而這種景象卻在近![]() 年出現了戲劇性的逆轉.統計顯示.2011年之前,方便面銷量在中國連續
年出現了戲劇性的逆轉.統計顯示.2011年之前,方便面銷量在中國連續![]() 年保持兩位數增長,2013年的年銷量更是創下
年保持兩位數增長,2013年的年銷量更是創下![]() 億包的輝煌戰績;但2013年以來,方便面銷量卻連續3年下跌,只剩
億包的輝煌戰績;但2013年以來,方便面銷量卻連續3年下跌,只剩![]() 億包,具體如下表.相較于方便面,網絡訂餐成為大家更加青睞的消費選擇.近年來,網絡訂餐市場規模的“井噴式”增長,也充分反映了人們消費方式的變化.
億包,具體如下表.相較于方便面,網絡訂餐成為大家更加青睞的消費選擇.近年來,網絡訂餐市場規模的“井噴式”增長,也充分反映了人們消費方式的變化.
全國方便面銷量情況(單位“億包/桶)(數據來源:世界方便面協會)
年份 |
|
|
|
|
時間代號 |
|
|
|
|
年銷量 |
|
|
|
|
(1)根據上表,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() .用所求回歸方程預測2017 年(
.用所求回歸方程預測2017 年(![]() )方便面在中國的年銷量;
)方便面在中國的年銷量;
(2)方便面銷量遭遇滑鐵盧受到哪些因素影響? 中國的消費業態發生了怎樣的轉變? 某媒體記者隨機對身邊的![]() 位朋友做了一次調查,其中
位朋友做了一次調查,其中![]() 位受訪者表示超過
位受訪者表示超過![]() 年未吃過方便面,
年未吃過方便面,![]() 位受訪者認為方便面是健康食品;而
位受訪者認為方便面是健康食品;而![]() 位受訪者有過網絡訂餐的經歷,現從這
位受訪者有過網絡訂餐的經歷,現從這![]() 人中抽取
人中抽取![]() 人進行深度訪談,記
人進行深度訪談,記![]() 表示隨機抽取的
表示隨機抽取的![]() 人認為方便面是健康食品的人數,求隨機變量
人認為方便面是健康食品的人數,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
參考公式:回歸方程:![]() ,其中
,其中 ,
,![]() .
.
參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方形![]() 的邊長為
的邊長為![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起,使平面
折起,使平面![]() 平面
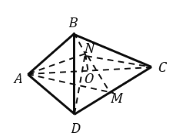
平面![]() ,得到如圖所示的三棱錐
,得到如圖所示的三棱錐![]() ,若
,若![]() 為
為![]() 邊的中點,
邊的中點,![]() 分別為
分別為![]() 上的動點(不包括端點),且
上的動點(不包括端點),且![]() ,設
,設![]() ,則三棱錐
,則三棱錐![]() 的體積取得最大值時,三棱錐
的體積取得最大值時,三棱錐![]() 的內切球的半徑為_______.
的內切球的半徑為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一款擊鼓小游戲的規則如下:每輪游戲都需擊鼓三次,每次擊鼓要么出現一次音樂,要么不出現音樂;每輪游戲擊鼓三次后,出現一次音樂獲得10分,出現兩次音樂獲得20分,出現三次音樂獲得100分,沒有出現音樂則扣除200分(即獲得-200分).設每次擊鼓出現音樂的概率為![]() ,且各次擊鼓是否出現音樂相互獨立.
,且各次擊鼓是否出現音樂相互獨立.
(1)玩三輪游戲,至少有一輪出現音樂的概率是多少?
(2)設每輪游戲獲得的分數為X,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年1月26日,甘肅省人民政府辦公廳發布《甘肅省關于餐飲業質量安全提升工程的實施意見》,衛生部對16所大學食堂的“進貨渠道合格性”和“食品安全”進行量化評估.滿10分者為“安全食堂”,評分7分以下的為“待改革食堂”.評分在4分以下考慮為“取締食堂”,所有大學食堂的評分在7~10分之間,以下表格記錄了它們的評分情況:

(1)現從16所大學食堂中隨機抽取3個,求至多有1個評分不低于9分的概率;
(2)以這16所大學食堂評分數據估計大學食堂的經營性質,若從全國的大學食堂任選3個,記![]() 表示抽到評分不低于9分的食堂個數,求
表示抽到評分不低于9分的食堂個數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有些事,有些人會永遠留在腦海,不會忘記,不會褪色.其實沒什么放不下的,只是會覺得,付出了這么多時間,卻始終沒有被感動......已知拋物線![]() ,且
,且![]() ,
,![]() ,
,![]() 三點中恰有兩點在拋物線
三點中恰有兩點在拋物線![]() 上,另一點是拋物線
上,另一點是拋物線![]() 的焦點.
的焦點.
(1)求證:![]() 、
、![]() 、
、![]() 三點共線;
三點共線;
(2)若直線![]() 過拋物線
過拋物線![]() 的焦點且與拋物線
的焦點且與拋物線![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 到
到![]() 軸的距離為
軸的距離為![]() ,點
,點![]() 到
到![]() 軸的距離為
軸的距離為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com