
(本題滿分18分)本題共有3個小題,第1小題滿分3分,第2小題滿分6分,第3小題滿分9分.
已知 的三個頂點在拋物線
的三個頂點在拋物線 :
: 上運動,
上運動,
(1). 求 的焦點坐標;
的焦點坐標;
(2). 若點 在坐標原點, 且
在坐標原點, 且 ,點
,點 在
在 上,且
上,且  ,
,
求點 的軌跡方程;
的軌跡方程;
(3). 試研究: 是否存在一條邊所在直線的斜率為 的正三角形
的正三角形 ,若存在,求出這個正三角形
,若存在,求出這個正三角形 的邊長,若不存在,說明理由.
的邊長,若不存在,說明理由.
(1) 【解】. 由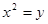 得
得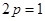 所以,焦點坐標為
所以,焦點坐標為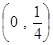 ……3分
……3分
(2) 【解1】設點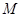 的坐標為
的坐標為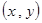 ,
,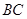 邊所在的方程為
邊所在的方程為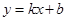 (
(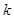 顯然存在的),與拋物線
顯然存在的),與拋物線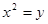 交于
交于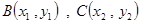
則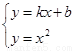 得
得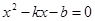 ,
,
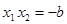 ……5分
……5分
又點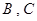 在拋物線
在拋物線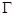 上,故有
上,故有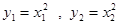 ,
, 
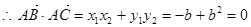
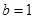 或
或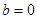 (舍)
(舍)
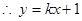 -------①
……7分
-------①
……7分
又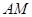 的斜率為
的斜率為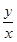 ,則有
,則有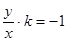 ,既
,既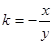 代入①
代入①
故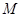 點軌跡為
點軌跡為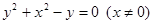 (注:沒寫
(注:沒寫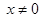 扣1分) ……9分
扣1分) ……9分
另解:由上式①過定點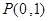 ,
,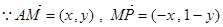
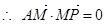 ,
,
所以, 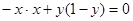 , 既
, 既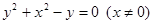
【解2】設點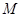 的坐標為
的坐標為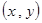 ,
,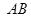 方程為
方程為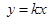 ,由
,由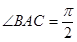 得
得 方程為
方程為
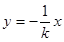 ,則
,則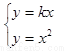 得
得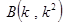 , 同理可得
, 同理可得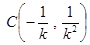
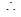
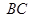 方程為
方程為 恒過定點
恒過定點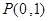 ,
,
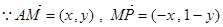
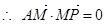 ,
,
所以, 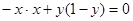 , 既
, 既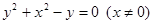
(注:沒寫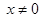 扣1分)
扣1分)
(其他解法,可根據【解1】的評分標準給分)
(3) 【解1】
若存在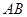 邊所在直線的斜率為
邊所在直線的斜率為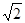 的正三角形
的正三角形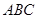 ,設
,設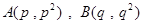 ,
,
(其中不妨設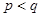 ), 則
), 則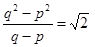 ,
, 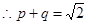 ------① ……11分
------① ……11分
令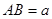 ,則
,則 ,即
,即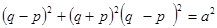
將①代入得, ,
,
 -----------------②
……13分
-----------------②
……13分
線段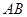 的中點為
的中點為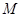 ,由①, ②得
,由①, ②得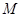 的橫坐標為
的橫坐標為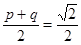 ,
,
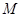 的縱坐標為
的縱坐標為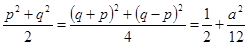 ……15分
……15分
又設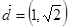 由
由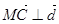 得
得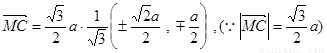
 點
點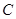 在拋物線
在拋物線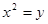 上,則
上,則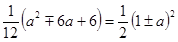 ,即
,即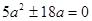 ,
,
又因為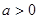 ,
, 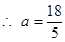 ……18分
……18分
設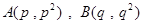 ,
,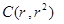
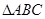 的三邊所在直線
的三邊所在直線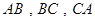 的斜率分別是
的斜率分別是
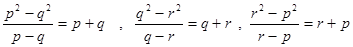 ------①
……12分
------①
……12分
若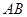 邊所在直線的斜率為
邊所在直線的斜率為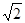 ,
,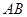 邊所在直線和
邊所在直線和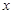 軸的正方向所成角為
軸的正方向所成角為
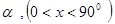 ,則
,則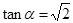 ,
,
所以 ……14分
……14分
即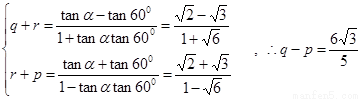 -----②
-----②
又 --------------③
……16分
--------------③
……16分
所以, 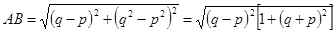
將②, ③代入上式得邊長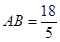 ……18分
……18分
(其他解法,可根據【解1】的評分標準給分)
【解析】略


科目:高中數學 來源: 題型:
(本題滿分18分,其中第1小題5分,第2小題5分,第3小題8分)
在平面直角坐標系中,已知![]() 為坐標原點,點
為坐標原點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,其中
,其中![]() 且
且![]() .設
.設![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在區間
在區間![]() 內的解集;
內的解集;
(2)若點![]() 是過點
是過點![]() 且法向量為
且法向量為![]() 的直線
的直線![]() 上的動點.當
上的動點.當![]() 時,設函數
時,設函數![]() 的值域為集合
的值域為集合![]() ,不等式
,不等式![]() 的解集為集合
的解集為集合![]() . 若
. 若![]() 恒成立,求實數
恒成立,求實數![]() 的最大值;
的最大值;
(3)根據本題條件我們可以知道,函數![]() 的性質取決于變量
的性質取決于變量![]() 、
、![]() 和
和![]() 的值. 當
的值. 當![]() 時,試寫出一個條件,使得函數
時,試寫出一個條件,使得函數![]() 滿足“圖像關于點
滿足“圖像關于點![]() 對稱,且在
對稱,且在![]() 處
處![]() 取得最小值”.(說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.)
取得最小值”.(說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.)
查看答案和解析>>
科目:高中數學 來源:上海市普陀區2010屆高三第二次模擬考試理科數學試題 題型:解答題
(本題滿分18分,其中第1小題5分,第2小題5分,第3小題8分)
在平面直角坐標系中,已知 為坐標原點,點
為坐標原點,點 的坐標為
的坐標為 ,點
,點 的坐標為
的坐標為 ,其中
,其中 且
且 .設
.設 .
.
(1)若 ,
, ,
, ,求方程
,求方程 在區間
在區間 內的解集;
內的解集;
(2)若點 是過點
是過點 且法向量為
且法向量為 的直線
的直線 上的動點.當
上的動點.當 時,設函數
時,設函數 的值域為集合
的值域為集合 ,不等式
,不等式 的解集為集合
的解集為集合 . 若
. 若 恒成立,求實數
恒成立,求實數 的最大值;
的最大值;
(3)根據本題條件我們可以知道,函數 的性質取決于變量
的性質取決于變量 、
、 和
和 的值. 當
的值. 當 時,試寫出一個條件,使得函數
時,試寫出一個條件,使得函數 滿足“圖像關于點
滿足“圖像關于點 對稱,且在
對稱,且在 處
處 取得最小值”.(說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.)
取得最小值”.(說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.)
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市長寧區高三教學質量測試理科數學 題型:解答題
(本小題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分.
(文)已知數列 中,
中,
(1)求證數列 不是等比數列,并求該數列的通項公式;
不是等比數列,并求該數列的通項公式;
(2)求數列 的前
的前 項和
項和 ;
;
(3)設數列 的前
的前 項和為
項和為 ,若
,若 對任意
對任意 恒成立,求
恒成立,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市長寧區高三教學質量測試理科數學 題型:解答題
本小題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分.
設函數 是定義域為R的奇函數.
是定義域為R的奇函數.
(1)求k值;
(2)(文)當 時,試判斷函數單調性并求不等式f(x2+2x)+f(x-4)>0的解集;
時,試判斷函數單調性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,試判斷函數單調性并求使不等式 恒成立的
恒成立的 的取值范圍;
的取值范圍;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值為-2,求m的值.
查看答案和解析>>
科目:高中數學 來源:上海市普陀區2010屆高三第二次模擬考試理科數學試題 題型:解答題
(本題滿分18分,其中第1小題5分,第2小題5分,第3小題8分)
在平面直角坐標系中,已知 為坐標原點,點
為坐標原點,點 的坐標為
的坐標為 ,點
,點 的坐標為
的坐標為 ,其中
,其中 且
且 .設
.設 .
.
(1)若 ,
, ,
, ,求方程
,求方程 在區間
在區間 內的解集;
內的解集;
(2)若點 是過點
是過點 且法向量為
且法向量為 的直線
的直線 上的動點.當
上的動點.當 時,設函數
時,設函數 的值域為集合
的值域為集合 ,不等式
,不等式 的解集為集合
的解集為集合 . 若
. 若 恒成立,求實數
恒成立,求實數 的最大值;
的最大值;
(3)根據本題條件我們可以知道,函數 的性質取決于變量
的性質取決于變量 、
、 和
和 的值. 當
的值. 當 時,試寫出一個條件,使得函數
時,試寫出一個條件,使得函數 滿足“圖像關于點
滿足“圖像關于點 對稱,且在
對稱,且在 處
處 取得最小值”.(說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.)
取得最小值”.(說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com