
【題目】對于函數![]() ,若關系式
,若關系式![]() 中變量
中變量![]() 是變量
是變量![]() 的函數,則稱函數
的函數,則稱函數![]() 為可變換函數.例如:對于函數
為可變換函數.例如:對于函數![]() ,若
,若![]() ,則
,則![]() ,所以變量
,所以變量![]() 是變量
是變量![]() 的函數,所以
的函數,所以![]() 是可變換函數.
是可變換函數.
(1)求證:反比例函數![]() 不是可變換函數;
不是可變換函數;
(2)試判斷函數![]() 是否是可變換函數并說明理由;
是否是可變換函數并說明理由;
(3)若函數![]() 為可變換函數,求實數
為可變換函數,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)見解析;(3)見解析.
【解析】分析:(1)利用反證法,假設![]() 是可變換函數,
是可變換函數,![]() ,利用關變量
,利用關變量![]() 的一元二次方程無解但導出矛盾,從而可得結論;(2)利用
的一元二次方程無解但導出矛盾,從而可得結論;(2)利用![]() 必須有交點,而
必須有交點,而![]() 連續且單調遞減,值域為
連續且單調遞減,值域為![]() ,
,![]() 連續且單調遞增,值域為
連續且單調遞增,值域為![]() ,進而可得結論;. (3)
,進而可得結論;. (3)![]() ,則
,則![]() 恒大于
恒大于![]() ,即無交點,不滿足題意;若
,即無交點,不滿足題意;若![]() ,則
,則![]() 必定有交點,即方程
必定有交點,即方程![]() 有解,從而可得結果.
有解,從而可得結果.
詳解:(1)假設![]() 是可變換函數,則
是可變換函數,則![]() ,
,
因為變量![]() 是任意的,故當
是任意的,故當![]() 時,此時有關變量
時,此時有關變量![]() 的一元二次方程無解,
的一元二次方程無解,
則與假設矛盾,故原結論正確,得證;
(2)若![]() 是可變換函數,則
是可變換函數,則![]() ,
,
則有關![]() 的兩個函數:
的兩個函數:![]() 必須有交點,而
必須有交點,而![]() 連續且單調遞減,值域為
連續且單調遞減,值域為![]() ,
,
![]() 連續且單調遞增,值域為
連續且單調遞增,值域為![]() ,所以這兩個函數
,所以這兩個函數![]() 與
與![]() 必定有交點,
必定有交點,
即:變量![]() 是變量
是變量![]() 的函數,所以
的函數,所以![]() 是可變換函數;
是可變換函數;
(3)函數![]() 為可變換函數,則
為可變換函數,則![]() ,
,
若![]() ,則
,則![]() 恒大于
恒大于![]() ,即無交點,不滿足題意;
,即無交點,不滿足題意;
若![]() ,則
,則![]() 必定有交點,即方程
必定有交點,即方程![]() 有解,從而滿足題意.
有解,從而滿足題意.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案科目:高中數學 來源: 題型:
【題目】設函數![]() ,給定數列
,給定數列![]() ,其中
,其中![]() ,
,![]() .
.
(1)若![]() 為常數數列,求a的值;
為常數數列,求a的值;
(2)當![]() 時,探究
時,探究![]() 能否是等比數列?若是,求出
能否是等比數列?若是,求出![]() 的通項公式;若不是,說明理由;
的通項公式;若不是,說明理由;
(3)設![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,當a=1時,求證:
,當a=1時,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,圓C的參數方程![]() (φ為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(φ為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(Ⅰ)求圓C的極坐標方程;
(Ⅱ)直線l的極坐標方程是ρ(sinθ+![]() )=3
)=3![]() ,射線OM:θ=
,射線OM:θ=![]() 與圓C的交點為O,P,與直線l的交點為Q,求線段PQ的長.
與圓C的交點為O,P,與直線l的交點為Q,求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=a+bx與![]() ,若對于任意一點
,若對于任意一點![]() ,過點
,過點![]() 作與X軸垂直的直線,交函數y=a+bx的圖象于點
作與X軸垂直的直線,交函數y=a+bx的圖象于點![]() ,交函數
,交函數![]() 的圖象于點
的圖象于點![]() ,定義:
,定義:![]() ,若
,若![]() 則用函數y=a+bx來擬合Y與X之間的關系更合適,否則用函數
則用函數y=a+bx來擬合Y與X之間的關系更合適,否則用函數![]() 來擬合Y與X之間的關系
來擬合Y與X之間的關系
(1)給定一組變量P1(1,4),P2(2,5),p3(3,6),p4(4,5.5),p5(5,5.6),p6(6,5.8),對于函數![]() 與函數
與函數![]() ,試利用定義求Q1,Q2的值,并判斷哪一個更適合作為點PI(xi,yi)(i=1,2,3…6)中的Y與X之間的擬合函數;
,試利用定義求Q1,Q2的值,并判斷哪一個更適合作為點PI(xi,yi)(i=1,2,3…6)中的Y與X之間的擬合函數;
(2)若一組變量的散點圖符合![]() 圖象,試利用下表中的有關數據與公式求y對x的回歸方程, 并預測當
圖象,試利用下表中的有關數據與公式求y對x的回歸方程, 并預測當![]() 時,
時,![]() 的值為多少.
的值為多少.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中的![]()
(附:對于一組數據![]() ,其回歸直線方程
,其回歸直線方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為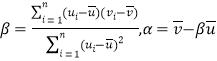 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,a為常數且a>0.
,a為常數且a>0.
(1)f(x)的圖象關于直線x= ![]() 對稱;
對稱;
(2)若x0滿足f(f(x0))=x0 , 但f(x0)≠x0 , 則x0稱為函數f(x)的二階周期點,如果f(x)有兩個二階周期點x1 , x2 , 試確定a的取值范圍;
(3)對于(2)中的x1 , x2 , 和a,設x3為函數f(f(x))的最大值點,A(x1 , f(f(x1))),B(x2 , f(f(x2))),C(x3 , 0),記△ABC的面積為S(a),討論S(a)的單調性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點(0,1),(3+2![]() ,0),(3-2
,0),(3-2![]() ,0)在圓C上.
,0)在圓C上.
(1)求圓C的方程.
(2)若圓C與直線x-y+a=0交于A,B兩點,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A是以BC為直徑的圓O上異于B,C的動點,P為平面ABC外一點,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,則三棱錐P﹣ABC外接球的表面積為______.
,則三棱錐P﹣ABC外接球的表面積為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一微商店對某種產品每天的銷售量(![]() 件)進行為期一個月的數據統計分析,并得出了該月銷售量的直方圖(一個月按30天計算)如圖所示.假設用直方圖中所得的頻率來估計相應事件發生的概率.
件)進行為期一個月的數據統計分析,并得出了該月銷售量的直方圖(一個月按30天計算)如圖所示.假設用直方圖中所得的頻率來估計相應事件發生的概率.

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)求日銷量的平均值(同一組中的數據用該組區間的中點值作代表);
(3)若微商在一天的銷售量超過25件(包括25件),則上級商企會給微商贈送100元的禮金,估計該微商在一年內獲得的禮金數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國倉儲指數是反映倉儲行業經營和國內市場主要商品供求狀況與變化趨勢的一套指數體系.如圖所示的折線圖是2017年和2018年的中國倉儲指數走勢情況.根據該折線圖,下列結論中不正確的是( )

A. 2018年1月至4月的倉儲指數比2017年同期波動性更大
B. 2017年、2018年的最大倉儲指數都出現在4月份
C. 2018年全年倉儲指數平均值明顯低于2017年
D. 2018年各月倉儲指數的中位數與2017年各月倉儲指數中位數差異明顯
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com