【題目】在2019迎新年聯歡會上,為了活躍大家氣氛,設置了“摸球中獎”游戲,桌子上放置一個不透明的箱子,箱子中有3個黃色、3個白色的乒乓球(其體積、質地完全相同)游戲規則：從箱子中隨機摸出3個球,若摸得同一顏色的3個球,摸球者中獎價值50元獎品;若摸得非同一顏色的3個球,摸球者中獎價值20元獎品.
(1)摸出的3個球為白球的概率是多少?
(2)假定有10人次參與游戲,試從概率的角度估算一下需要準備多少元錢購買獎品?
【答案】（1）0.05（2）230元
【解析】
（1）把3個黃色乒乓球標記為
、
、
，
個白色的乒乓球標記為
、
、，列舉出所有的基本事件，并確定基本事件的總數，并找出事件“摸出的個球都為白球”所包含的事件及數目，再利用古典概型的概率公式可計算出所求事件的概率；
（2）計算出事件“摸出三個顏色相同的球”的概率為
，于此得知
次試驗中有次摸出三個同顏色的球，于是得出購買獎品的錢為
。
（1）把3個黃色乒乓球標記為
,3個白色的乒乓球標記為1,2,3
從6個球中隨機摸出3個的基本事件為:
，共20個，
事件
{摸出的3個球為白球}，事件
包含的基本事件有1個，即摸出123，
∴
；
（2）事件
{摸出的3個球為同一顏色}={摸出的3個球為白球或摸出的3個球為黃球}
∴
，
假定有10人次參與游戲摸獎，由摸出的3個球為同一顏色的概率可估計事件
發生有1次，不發生9次，
則需要準備
元錢購買獎品.
文敬圖書課時先鋒系列答案科目：高中數學 來源： 題型：
【題目】如圖，A、B、C為⊙O上三點，B為 
的中點，P為AC延長線上一點，PQ與⊙O相切于點Q，BQ與AC相交于點D．
（Ⅰ）證明：△DPQ為等腰三角形；
（Ⅱ）若PC=1，AD=PD，求BDQD的值．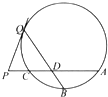
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】扇形AOB中心角為
，所在圓半徑為
，它按如圖(Ⅰ)(Ⅱ)兩種方式有內接矩形CDEF．
(1)矩形CDEF的頂點C、D在扇形的半徑OB上，頂點E在圓弧AB上，頂點F在半徑OA上，設
；
(2)點M是圓弧AB的中點，矩形CDEF的頂點D、E在圓弧AB上，且關于直線OM對稱，頂點C、F分別在半徑OB、OA上，設
；
試研究(1)(2)兩種方式下矩形面積的最大值，并說明兩種方式下哪一種矩形面積最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的上、下焦點分別為
，上焦點
到直線
的距離為3，橢圓
的離心率
.
（1）求橢圓的方程；
（2）橢圓
，設過點
斜率存在且不為0的直線交橢圓
于
兩點，試問
軸上是否存在點
，使得
？若存在，求出點的坐標；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-4：坐標系與參數方程]
在直角坐標系
中，曲線
的參數方程為
（
為參數），以原點
為極點，
軸的正半軸為極軸建立極坐標系.
(1)求曲線的極坐標方程；
(2)若點
的極坐標為
，
是曲線上的一動點，求
面積的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
