
【題目】如圖甲,直角梯形![]() 中,
中, ![]() ,
, ![]() ,點
,點![]() 分別在
分別在![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() ,現將梯形
,現將梯形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 與平面
與平面![]() 垂直(如圖乙).
垂直(如圖乙).
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
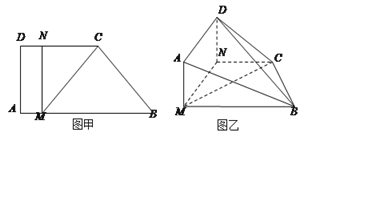
(II)當![]() 的長為何值時,二面角
的長為何值時,二面角![]() 的大小為
的大小為![]() ?
?
【答案】(Ⅰ)見解析;(Ⅱ) ![]() .
.
【解析】試題分析:
(1)建立空間直角坐標系,結合直線的方向向量和平面的一個法向量即可證得線面平行;
(2)結合空間直角坐標系探究可得![]() 時,二面角
時,二面角![]() 的大小為
的大小為![]() .
.
試題解析:
(Ⅰ)如圖建立空間直角坐標系N-xyz.
設![]() ,則A(2,0,t),B(2,4,0),
,則A(2,0,t),B(2,4,0), ![]()
又易知平面DNC的一個法向量為![]() ,
,
由![]() ,得AB∥平面DNC.
,得AB∥平面DNC.
(Ⅱ)設![]() ,則D(0,0,t),C(0,2,0),B(2,4,0),故
,則D(0,0,t),C(0,2,0),B(2,4,0),故![]() (0,-2,t),
(0,-2,t), ![]() (2,2,0),
(2,2,0),
設平面DBC的一個法向量為![]() ,則
,則![]()
取![]() ,則
,則![]() ,即
,即![]() ,
,
又易知平面BCN的一個法向量為![]() ,
,
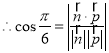 ,即
,即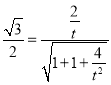 ,解得
,解得![]() .
.
另解:(Ⅰ)∵MB∥NC,MB![]() 平面DNC,NC
平面DNC,NC![]() 平面DNC,
平面DNC,
∴MB∥平面DNC. 同理MA∥平面DNC,
又MA∩MB=M且MA、MB![]() 平面MAB,
平面MAB,
∴平面MAB∥平面NCD, 又AB![]() 平面MAB,
平面MAB,
∴AB∥平面NCD.
(Ⅱ)過N作NH⊥BC交BC延長線于H,連結DH,
∵平面AMND⊥平面MNCB,DN⊥MN
∴DN⊥平面MNCB,從而DH⊥BC,
∴∠DHN為二面角D-BC-N的平面角.
由已知得, ![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() .
.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】拋物線C:y2=2px(p>0)的準線為l,焦點為F.⊙M的圓心在x軸的正半軸上,且與y軸相切.過原點O作傾斜角為![]() 的直線n交l于點A, 交⊙M于另一點B,且AO=OB=2.
的直線n交l于點A, 交⊙M于另一點B,且AO=OB=2.
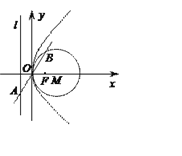
(1)求⊙M和拋物線C的方程;
(2)若P為拋物線C上的動點,求![]() 的最小值;
的最小值;
(3)過l上的動點Q向⊙M作切線,切點為S,T,求證:直線ST恒過一個定點,并求該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M={(x,y)|y=f(x)},若對于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,則稱集合M是“垂直對點集”.給出下列四個集合:
①M={![]() };②M={(x,y)|y=sinx+1};
};②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};④M={(x,y)|y=ex﹣2}.
其中是“垂直對點集”的序號是( )
A. ①② B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C的一個焦點為![]() ,對應于這個焦點的準線方程為
,對應于這個焦點的準線方程為![]()
(1)寫出拋物線C的方程;
(2)過F點的直線與曲線C交于A、B兩點,O點為坐標原點,求△AOB重心G的軌跡方程;
(3)點P是拋物線C上的動點,過點P作圓![]() 的切線,切點分別是M,N.當P點在何處時,|MN|的值最小?求出|MN|的最小值.
的切線,切點分別是M,N.當P點在何處時,|MN|的值最小?求出|MN|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. “![]() 為真”是“
為真”是“![]() 為真”的充分不必要條件;
為真”的充分不必要條件;
B. 樣本![]() 的標準差是3.3;
的標準差是3.3;
C. K2是用來判斷兩個分類變量是否相關的隨機變量,當K2的值很小時可以推定兩類變量不相關;
D. 設有一個回歸直線方程為![]() ,則變量
,則變量![]() 每增加一個單位,
每增加一個單位,![]() 平均減少1.5個單位.
平均減少1.5個單位.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)當x∈[1,2]時,求f(x)的最大值.
(3)m為何值時,函數g(x)=ax的圖象與h(x)=bx﹣m的圖象恒有兩個交點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行有獎促銷活動,顧客購買一定金額商品后即可抽獎,每次抽獎都從裝有4個紅球、6個白球的甲箱和裝有5個紅球、5個白球的乙箱中,各隨機摸出1個球,在摸出的2個球中,若都是紅球,則獲一等獎;若只有1個紅球,則獲二等獎;若沒有紅球,則不獲獎.
(1)求顧客抽獎1次能獲獎的概率;
(2)若某顧客有3次抽獎機會,記該顧客在3次抽獎中獲一等獎的次數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com