
某市規定,高中學生三年在校期間參加不少于 小時的社區服務才合格.教育部門在全市隨機抽取200位學生參加社區服務的數據,按時間段
小時的社區服務才合格.教育部門在全市隨機抽取200位學生參加社區服務的數據,按時間段 ,
, ,
, ,
, ,
, (單位:小時)進行統計,其頻率分布直方圖如圖所示.
(單位:小時)進行統計,其頻率分布直方圖如圖所示.
(Ⅰ)求抽取的200位學生中,參加社區服務時間不少于90小時的學生人數,并估計
從全市高中學生中任意選取一人,其參加社區服務時間不少于90小時的概率;
(Ⅱ)從全市高中學生(人數很多)中任意選取3位學生,記 為3位學生中參加社區服務時間不少于90小時的人數.試求隨機變量
為3位學生中參加社區服務時間不少于90小時的人數.試求隨機變量 的分布列和數學期望
的分布列和數學期望 .
.
(Ⅰ)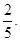 (Ⅱ)
(Ⅱ)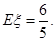

0 1 2 3 
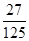
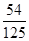
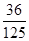
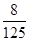
解析試題分析:(Ⅰ)根據頻率分布直方圖中小長方形面積為頻率,而頻數為總數與頻率之積. 因此參加社區服務時間在時間段 小時的學生人數為
小時的學生人數為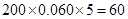 (人),參加社區服務時間在時間段
(人),參加社區服務時間在時間段 小時的學生人數為
小時的學生人數為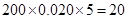 (人).所以抽取的200位學生中,參加社區服務時間不少于90小時的學生人數為
(人).所以抽取的200位學生中,參加社區服務時間不少于90小時的學生人數為 人.概率估計為
人.概率估計為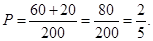 (Ⅱ)隨機變量
(Ⅱ)隨機變量 的可能取值為
的可能取值為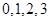 .由(Ⅰ)可知,概率為
.由(Ⅰ)可知,概率為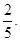 因為
因為  ~
~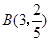 ,所以
,所以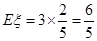 .隨機變量
.隨機變量 的分布列為
的分布列為
0 1 2 3 
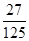
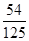
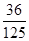
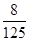
解:(Ⅰ)根據題意,
參加社區服務時間在時間段 小時的學生人數為
小時的學生人數為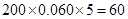 (人),
(人),
參加社區服務時間在時間段 小時的學生人數為
小時的學生人數為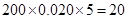 (人).
(人).
所以抽取的200位學生中,參加社區服務時間不少于90小時的學生人數為 人.
人.
所以從全市高中學生中任意選取一人,其參加社區服務時間不少于90小時的
概率估計為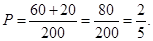 5分
5分
(Ⅱ)由(Ⅰ)可知,從全市高中生中任意選取1人,其參加社區服務時間不少于90小時的概率為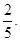
由已知得,隨機變量 的可能取值為
的可能取值為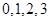 .
.
所以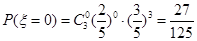 ;
;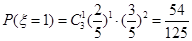 ;
;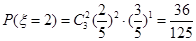 ;
; .
.
隨機變量 的分布列為
的分布列為