
【題目】某單位對一崗位面向社會公開招聘,若甲筆試成績與面試成績至少有一項比乙高,則稱甲不亞于乙.在18位應聘者中,如果某應聘者不亞于其他17人,則稱其為“優秀人才”.那么這18人中“優秀人才”數最多為( )
A. 1 B. 2 C. 9 D. 18
【答案】D
【解析】先考慮兩個應聘者的情形,如果甲的筆試成績>乙的筆試成績,且乙的面試成績>甲的面試成績,可知“優秀人才”最多有2人.
再考慮三個應聘者的情形,如果甲的筆試成績>乙的筆試成績>丙的筆試成績,且丙的面試成績>乙的面試成績>甲的面試成績,可知“優秀人才”最多有3人.
由此可以設想,當有18個應聘者時,設每個應聘者為Ai,(i=1,2,…,100),其筆試成績為xi,面試成績為yi,當 ![]() 且
且![]() 時,由筆試成績看,Ai不亞于Ai+1,Ai+2,…,A100;
時,由筆試成績看,Ai不亞于Ai+1,Ai+2,…,A100;
由面試成績看,Ai不亞于Ai-1,Ai-2,…,A1 所以,Ai不亞于其他17人(i=1,2,…,18)所以,Ai為“優秀人才”(i=1,2,…,18)
因此,18個應聘者中的“優秀人才”最多可能有 18個.
故選D.


科目:高中數學 來源: 題型:
【題目】現有年齡在25到55歲的一群人身體上的某項數據,其頻率分布直方圖如下.(注:每組包括左端點,不包括右端點)

(1)請補全頻率分布直方圖;
(2)估計年齡的平均數;(精確到小數點后一位數字)
(3)若50到55歲的人數是50,現在想要從25到35歲的人群中用分層抽樣的方法抽取30人,那么25到30歲這一組人中應該抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的偶函數,且當x≥0時,f(x)=loga(x+1)(a>0,且a≠1).
(1)求函數f(x)的解析式;
(2)若-1<f(1)<1,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() x3-
x3-![]() ax2,a∈R.
ax2,a∈R.
(1)當a=2時,求曲線y=f(x)在點(3,f(3))處的切線方程;
(2)設函數g(x)=f(x)+(x-a)cos x-sin x,討論g(x)的單調性并判斷有無極值,有極值時求出極值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產一種機器的固定成本為0.5萬元,但每生產100臺,需要加可變成本(即另增加投入)0.25萬元,市場對此產品的年求量為500臺,銷售的收入函數為![]() (萬元)(
(萬元)(![]() ),其中
),其中![]() 是產品售出的數量(單位:百臺).
是產品售出的數量(單位:百臺).
(1)把利潤表示為年產量的函數;
(2)年產量是多少時,工廠所得利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C過點M(0,-2)、N(3,1),且圓心C在直線x+2y+1=0上.
(1)求圓C的方程;
(2)設直線ax-y+1=0與圓C交于A,B兩點,是否存在實數a,使得過點P(2,0)的直線l垂直平分弦AB?若存在,求出實數a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年是新中國成立70周年,也是全面建成小康社會的關鍵之年.為喜迎祖國70周年生日,全民齊心奮力建設小康社會,某校特舉辦“喜迎國慶,共建小康”知識競賽活動.下面的莖葉圖是參賽兩組選手的答題得分情況,則下列說法正確的是( )
甲 | 乙 | |||||
5 | 7 | 7 | ||||
7 | 3 | 2 | 8 | 3 | 4 | 5 |
3 | 9 | 1 | ||||
A.甲組選手得分的平均數小于乙組選手得分的平均數.
B.甲組選手得分的中位數大于乙組選手得分的平均數.
C.甲組選手得分的中位數等于乙組選手得分的中位數.
D.甲組選手得分的方差大于乙組選手得分的方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
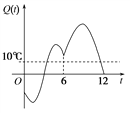
【題目】某地一年的氣溫Q(t)(單位:℃)與時間t(月份)之間的關系如圖所示,已知該年的平均氣溫為10 ℃,令C(t)表示時間段[0,t]的平均氣溫,下列四個函數圖象中,最能表示C(t)與t之間的函數關系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心
的圓心![]() 在拋物線
在拋物線![]() 上,圓
上,圓![]() 過原點且與拋物線的準線相切.
過原點且與拋物線的準線相切.
(1)求該拋物線的方程;
(2)過拋物線焦點![]() 的直線
的直線![]() 交拋物線于
交拋物線于![]() ,
, ![]() 兩點,分別在點
兩點,分別在點![]() ,
, ![]() 處作拋物線的兩條切線交于
處作拋物線的兩條切線交于![]() 點,求三角形
點,求三角形![]() 面積的最小值及此時直線
面積的最小值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com