Question

【題目】已知函數f（x）=2x+ax2+bcosx在點 處的切線方程為 ．
（Ⅰ）求a，b的值，并討論f（x）在 上的增減性；
（Ⅱ）若f（x1）=f（x2），且0＜x1＜x2＜π，求證： ．
（參考公式： ）

Answer 1

【答案】解：（Ⅰ）由題意知f'（x）=2+2ax﹣bsinx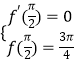，∴ 解得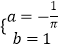
故 ， ．
當 時，f'（x）為減函數，且 ，
∴f'（x）＞0，f（x）為增函數．
（Ⅱ）證明：由f（x1）=f（x2），得 ，
所以 ，
兩邊同除以x1﹣x2 ， 得 ，
所以 ，
令 ，得 ，
得 ．
因為 ，
所以 ，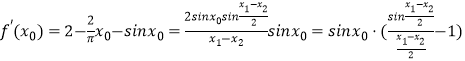
因為 ，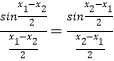
又 ，易知 ，所以 ，
又x0∈（0，π），所以sinx0＞0，故f'（x0）＜0，得 ．
【解析】（Ⅰ）求導數，利用函數f（x）=2x+ax2+bcosx在點 處的切線方程為 ，建立方程，求a，b的值，利用導數的正負討論f（x）在 上的增減性；（Ⅱ）令 ，得 ，得 ，證明sinx0＞0，故f'（x0）＜0，即可得出結論．