【題目】已知拋物線
的焦點為F，過F點的直線交拋物線于不同的兩點A、B，且
，點A關(guān)于
軸的對稱點為
，線段
的中垂線交軸于點D，則D點的坐標為
A. (2，0)B. (3，0)C. (4，0)D. (5，0)
【答案】D
【解析】
F的坐標為（1，0），設(shè)l的方程為y＝k（x﹣1）代入拋物線y2＝4x，設(shè)A（x1，y1），B（x2，y2），利用韋達定理以及拋物線的定義，求出k，即可求解直線
的方程．再寫出 的中垂線方程，令
即可求出D點坐標。
解：F的坐標為（1，0），
設(shè)
的方程為y＝k（x﹣1）代入拋物線y2＝4x得k2x2﹣（2k2+4）x+k2＝0，
由題意知k≠0，且[﹣（2k2+4）]2﹣4k2k2＝16（k2+1）＞0，
設(shè)A（x1，y1），B（x2，y2），∴
，x1x2＝1，
由拋物線的定義知|AB|＝x1+x2+2＝8，
∴
，∴k2＝1，即k＝±1，∴直線的方程為y＝±（x﹣1）．
，B（x2，y2），則其中點坐標為
直線
的斜率為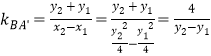
，
則其中垂線斜率為
∴直線 的中垂線方程為
令 ，得
，
D點坐標為（5,0）
故選D.
小天才課時作業(yè)系列答案
一課四練系列答案
黃岡小狀元滿分沖刺微測驗系列答案
新輔教導學系列答案科目：高中數(shù)學 來源： 題型：
【題目】在某區(qū)“創(chuàng)文明城區(qū)”
簡稱“創(chuàng)城”
活動中，教委對本區(qū)A，B，C，D四所高中校按各校人數(shù)分層抽樣調(diào)查，將調(diào)查情況進行整理后制成如表：
學校 | A | B | C | D |
抽查人數(shù) | 50 | 15 | 10 | 25 |
“創(chuàng)城”活動中參與的人數(shù) | 40 | 10 | 9 | 15 |
注：參與率是指：一所學校“創(chuàng)城”活動中參與的人數(shù)與被抽查人數(shù)的比值
假設(shè)每名高中學生是否參與“創(chuàng)城”活動是相互獨立的．
Ⅰ若該區(qū)共2000名高中學生，估計A學校參與“創(chuàng)城”活動的人數(shù)；
Ⅱ在隨機抽查的100名高中學生中，從A，C兩學校抽出的高中學生中各隨機抽取1名學生，求恰有1人參與“創(chuàng)城”活動的概率；
Ⅲ若將表中的參與率視為概率，從A學校高中學生中隨機抽取3人，求這3人參與“創(chuàng)城”活動人數(shù)的分布列及數(shù)學期望．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
的焦點
恰好是橢圓
的右焦點.
（1）求實數(shù)
的值及拋物線
的準線方程；
（2）過點任作兩條互相垂直的直線分別交拋物線于
、
和
、
點，求兩條弦的弦長之和
的最小值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為了調(diào)查民眾對國家實行“新農(nóng)村建設(shè)”政策的態(tài)度，現(xiàn)通過網(wǎng)絡問卷隨機調(diào)查了年齡在20周歲至80周歲的100人，他們年齡頻數(shù)分布和支持“新農(nóng)村建設(shè)”人數(shù)如下表：
年齡 |
|
|
|
|
|
|
頻數(shù) | 10 | 20 | 30 | 20 | 10 | 10 |
支持“新農(nóng)村建設(shè)” | 3 | 11 | 26 | 12 | 6 | 2 |
（1）根據(jù)上述統(tǒng)計數(shù)據(jù)填下面的
列聯(lián)表，并判斷是否有
的把握認為以50歲為分界點對“新農(nóng)村建設(shè)”政策的支持度有差異；
年齡低于50歲的人數(shù) | 年齡不低于50歲的人數(shù) | 合計 | |
支持 | |||
不支持 | |||
合計 |
（2）現(xiàn)從年齡在
內(nèi)的5名被調(diào)查人中任選兩人去參加座談會，求選出兩人中恰有一人支持新農(nóng)村建設(shè)的概率.
參考數(shù)據(jù)：
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
參考公式：
，其中
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
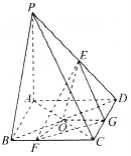
【題目】如圖所示，在底面為正方形的四棱錐P—ABCD中，AB=2，PA=4，PB=PD=
，AC與BD相交于點O，E，G分別為PD，CD中點，
(1)求證：EO//平面PBC；
(2)設(shè)線段BC上點F滿足BC=3BF，求三棱錐E—OFG的體積．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在三棱錐P﹣ABC中，AB＝1，BC＝2，AC
，PC
，PA，PB
，E是線段BC的中點．
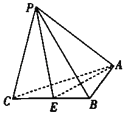
（1）求點C到平面APE的距離d；
（2）求二面角P﹣EA﹣B的余弦值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系xOy中，已知△ABC三個頂點坐標為A(7，8)，B(10，4)，C(2，－4)．
(1)求BC邊上的中線所在直線的方程；
(2)求BC邊上的高所在直線的方程．
【答案】（1）
；（2）
【解析】試題分析：（1）根據(jù)中點坐標公式求出
中點
的坐標，根據(jù)斜率公式可求得
的斜率，利用點斜式可求
邊上的中線所在直線的方程；（2）先根據(jù)斜率公式求出
的斜率，從而求出
邊上的高所在直線的斜率為
，利用點斜式可求
邊上的高所在直線的方程.
試題解析：（1）由B(10，4)，C(2，－4)，得BC中點D的坐標為（6，0），
所以AD的斜率為k＝
＝8，
所以BC邊上的中線AD所在直線的方程為y－0＝8(x－6)，
即8x－y－48＝0．
（2）由B(10，4)，C(2，－4)，得BC所在直線的斜率為k＝＝1，
所以BC邊上的高所在直線的斜率為－1，
所以BC邊上的高所在直線的方程為y－8＝－(x－7)，即x＋y－15＝0．
【題型】解答題
【結(jié)束】
17
【題目】已知直線l：x－2y＋2m－2＝0．
(1)求過點(2，3)且與直線l垂直的直線的方程；
(2)若直線l與兩坐標軸所圍成的三角形的面積大于4，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，四棱錐PABC中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M為線段AD上一點，AM=2MD，N為PC的中點.
（Ⅰ）證明MN∥平面PAB;
（Ⅱ）求直線AN與平面PMN所成角的正弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
