
當 為正整數(shù)時,定義函數(shù)
為正整數(shù)時,定義函數(shù)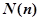 表示
表示 的最大奇因數(shù).如
的最大奇因數(shù).如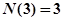 ,
,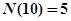 ,….記
,….記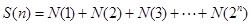 .則
.則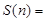 .(用
.(用 來表示)
來表示)
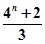
解析試題分析:由N(x)的性質(zhì)可得知,當x是奇數(shù)時,x的最大奇數(shù)因子明顯是它本身.因此N(x)=x,因此,我們就可將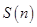 進行分解,分別算出奇數(shù)項的和與偶數(shù)項的和進而相加,即
進行分解,分別算出奇數(shù)項的和與偶數(shù)項的和進而相加,即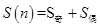 ,
,
所以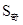 =N(1)+N(3)+…+N(
=N(1)+N(3)+…+N(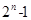 )=1+3+…+
)=1+3+…+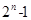 =
= 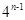 。
。
當x是偶數(shù)時,且x∈[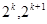 )
)
①當k=1時,x∈[2,4)該區(qū)間包含的偶數(shù)只有2,而N(2)=1所以該區(qū)間所有的偶數(shù)的最大奇因數(shù)之和為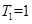 ;
;
②當k=2時,x∈[4,8),該區(qū)間包含的偶數(shù)為4,6,所以該區(qū)間所有的最大奇因數(shù)偶數(shù)之和為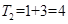
③當k=3時,x∈[8,16),該區(qū)間包含的偶數(shù)為8,10.,12,14,則該區(qū)間所有偶數(shù)的最大奇因數(shù)之和為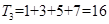 ,因此我們可以用數(shù)學(xué)歸納法得出當x∈[
,因此我們可以用數(shù)學(xué)歸納法得出當x∈[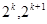 )該區(qū)間所有偶數(shù)的最大奇因數(shù)和
)該區(qū)間所有偶數(shù)的最大奇因數(shù)和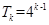
∴對k從1到n-1求和得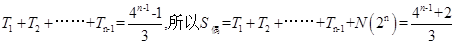 ,
,
綜上知: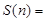
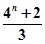 。
。
考點:數(shù)列的綜合應(yīng)用。
點評:本題主要考查了數(shù)列的求和問題.考查了學(xué)生通過已知條件分析問題和解決問題的能力.


科目:高中數(shù)學(xué) 來源: 題型:填空題
如圖所示的數(shù)陣叫“萊布尼茲調(diào)和三角形”,他們是由整數(shù)的倒數(shù)組成的,第 行有
行有 個數(shù)且兩端的數(shù)均為
個數(shù)且兩端的數(shù)均為 ,每個數(shù)是它下一行左右相鄰兩數(shù)的和,如:
,每個數(shù)是它下一行左右相鄰兩數(shù)的和,如: …,則第
…,則第 行第3個數(shù)字是 .
行第3個數(shù)字是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
蜜蜂被認為是自然界中最杰出的建筑師,單個蜂巢可以近似地看作是一個正六邊形,如圖為一組蜂巢的截面圖. 其中第一個圖有1個蜂巢,第二個圖有7個蜂巢,第三個圖有19個蜂巢,按此規(guī)律,以 表示第
表示第 幅圖的蜂巢總數(shù).則
幅圖的蜂巢總數(shù).則 =_____;
=_____; =___________.
=___________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
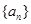 是公比為q的等比數(shù)列,其前n項的積為
是公比為q的等比數(shù)列,其前n項的積為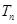 ,并且滿足條件
,并且滿足條件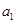 >1,
>1,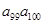 >1,
>1, 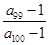 <0,給出下列結(jié)論:① 0<q<1;② T198<1;③
<0,給出下列結(jié)論:① 0<q<1;② T198<1;③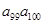 >1。其中正確結(jié)論的序號是 。
>1。其中正確結(jié)論的序號是 。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知數(shù)列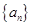 滿足對任意的
滿足對任意的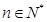 ,都有
,都有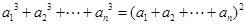 且
且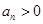 .
.
(1)求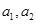 的值;
的值;
(2)求數(shù)列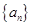 的通項公式
的通項公式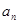 ;
;
(3)設(shè)數(shù)列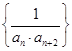 的前
的前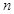 項和為
項和為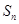 ,不等式
,不等式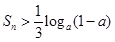 對任意的正整數(shù)
對任意的正整數(shù)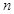 恒成立,求實數(shù)
恒成立,求實數(shù)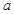 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù)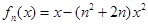 (其中
(其中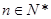 ),區(qū)間
),區(qū)間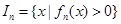 .
.
(1)求區(qū)間 的長度(注:區(qū)間
的長度(注:區(qū)間 的長度定義為
的長度定義為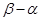 );
);
(2)把區(qū)間 的長度記作數(shù)列
的長度記作數(shù)列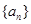 ,令
,令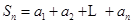 ,證明:
,證明: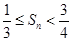 .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com