Question

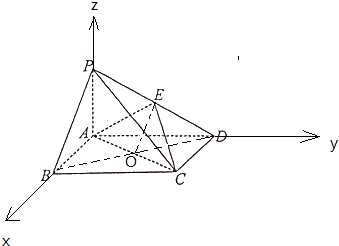
【題目】如圖，在四棱錐P﹣ABCD中，底面ABCD為矩形，PA⊥平面ABCD，E為PD的中點．

（1）證明：PB∥平面AEC；
（2）已知AP=AB=1，AD= ，求二面角D﹣AE﹣C的余弦值．

Answer 1

【答案】
（1）證明：連結AC、BD，交于點O，連結OE，

∵底面ABCD為矩形，∴O是BD中點，

∵E為PD的中點，∴OE∥PB，

∵PB平面AEC，OE平面AEC，

∴PB∥平面AEC．

（2）解：以A為原點，AB為x軸，AD為y軸，AP為z軸，建立空間直角坐標系，

∵AP=AB=1，AD= ，

∴A（0，0，0），C（1， ，0），P（0，0，1），D（0， ，0），E（0， ， ），

=（1， ，0）， =（0， ， ），

設平面AEC的法向量 =（x，y，z），

則 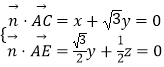，取x=3，得 =（3，﹣ ，3），

又平面DEA的法向理 =（1，0，0），

設二面角D﹣AE﹣C的平面角為θ，

則cosθ= = = ．

∴二面角D﹣AE﹣C的余弦值為 ．

【解析】（1）連結AC、BD，交于點O，連結OE，則OE∥PB，由此能證明PB∥平面AEC．（2）以A為原點，AB為x軸，AD為y軸，AP為z軸，建立空間直角坐標系，利用向量法能求出二面角D﹣AE﹣C的余弦值．
【考點精析】關于本題考查的直線與平面平行的判定，需要了解平面外一條直線與此平面內的一條直線平行，則該直線與此平面平行；簡記為：線線平行，則線面平行才能得出正確答案．