Question

已知函數f(x)＝e^x，a，b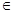R，且a＞0．
⑴若a＝2，b＝1，求函數f(x)的極值；
⑵設g(x)＝a(x－1)e^x－f(x)．
①當a＝1時，對任意x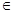 (0，＋∞)，都有g(x)≥1成立，求b的最大值；
②設g′(x)為g(x)的導函數．若存在x＞1，使g(x)＋g′(x)＝0成立，求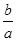的取值范圍．

Answer 1

⑴f (x)的極大值是f (－1)＝e^－1，f (x)的極小值是f (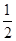)＝4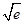;⑵① －1－e^－1 ;②（－1，＋∞）．

解析試題分析： ⑴由 a＝2，b＝1得，f (x)＝(2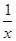＋)e^x, 定義域為(－∞，0)∪(0，＋∞);從而可求得 f ′(x)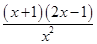＝e^x, 令f ′(x)＝0，得x₁＝－1，x₂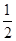＝，列表可求得f (x)的極值.
⑵①當a＝1時，g (x)＝(x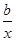－－2)e^x,由已知得不等式g (x)≥1在x∈（0，＋∞）上恒成立,即b≤x²－2x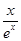－在x∈（0，＋∞）上恒成立,從而b≤(x²－2x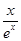－)_min x∈(0，＋∞）,令h(x)＝x²－2x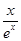－（x＞0）利用函數導數求出h(x)的最小值即可.
②由于g (x)＝(ax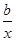－－2a)e^x，所以g 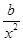′(x)＝(＋ax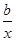－－a)e^x; 由g (x)＋g ′(x)＝0，得(ax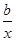－－2a)e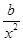^x＋(＋ax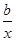－－a)e^x＝0，整理得2ax³－3ax²－2bx＋b＝0．
存在x＞1，使g (x)＋g ′(x)＝0成立，等價于存在x＞1，2ax³－3ax²－2bx＋b＝0成立．
注意到a＞0，所以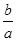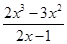＝（x＞1）;設u(x)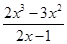＝（x＞1），則問題等價于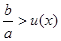的最小值(或下確界),利用函數導數可判斷u(x)在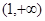上的單調性可求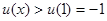得從而可得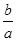的取值范圍為（－1，＋∞）．
試題解析：⑴當a＝2，b＝1時，f (x)＝(2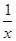＋)e^x，定義域為(－∞，0)∪(0，＋∞)．
所以f ′(x)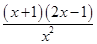＝e^x．令f ′(x)＝0，得x₁＝－1，x₂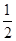＝，列表

x	(－∞，－1)	－1	(－1，0)	(0，)		(，＋∞)
f ′(x)			－	－
f (x)