
【題目】已知sinα+cosα= ![]() ,α∈(0,
,α∈(0, ![]() ),sin(β﹣
),sin(β﹣ ![]() )=
)= ![]() ,β∈(
,β∈( ![]() ,
, ![]() ).
).
(1)求sin2α和tan2α的值;
(2)求cos(α+2β)的值.
【答案】
(1)解:由題意得(sinα+cosα)2= ![]() ,
,
即1+sin2α= ![]() ,∴sin2α=
,∴sin2α= ![]() .
.
又2α∈(0, ![]() ),∴cos2α=
),∴cos2α= ![]() =
= ![]() ,∴tan2α=
,∴tan2α= ![]() =
= ![]()
(2)解:∵β∈( ![]() ,
, ![]() ),β﹣
),β﹣ ![]() ∈(0,
∈(0, ![]() ),∴cos(β﹣
),∴cos(β﹣ ![]() )=
)= ![]() ,
,
于是sin2(β﹣ ![]() )=2sin(β﹣
)=2sin(β﹣ ![]() )cos(β﹣
)cos(β﹣ ![]() )=
)= ![]() .
.
又sin2(β﹣ ![]() )=﹣cos2β,∴cos2β=﹣
)=﹣cos2β,∴cos2β=﹣ ![]() .
.
又2β∈( ![]() ,π),∴sin2β=
,π),∴sin2β= ![]() .
.
又cos2α= ![]() =
= ![]() ,
,
∴cosα= ![]() ,sinα=
,sinα= ![]() (α∈(0,
(α∈(0, ![]() )).
)).
∴cos(α+2β)=cosαcos2β﹣sinαsin2β
= ![]() ×(﹣
×(﹣ ![]() )﹣
)﹣ ![]() ×
× ![]() =﹣
=﹣ ![]()
【解析】(1)把已知條件兩邊平方,然后利用同角三角函數間的關系及二倍角的正弦函數公式化簡可得sin2α的值,根據2α的范圍利用同角三角函數間的關系求出cos2α即可得到tan2α的值;(2)根據β的范圍求出 ![]() 的范圍,由sin(
的范圍,由sin( ![]() )的值利用同角三角函數間的關系求出cos(
)的值利用同角三角函數間的關系求出cos( ![]() )的值,然后利用二倍角的正弦函數公式及同角三角函數間的關系分別求出sin2β和cos2β的值,根據第一問分別求出sinα和cosα的值,把所求的式子利用兩角和的余弦函數公式化簡后,將每個三角函數值代入即可求出.
)的值,然后利用二倍角的正弦函數公式及同角三角函數間的關系分別求出sin2β和cos2β的值,根據第一問分別求出sinα和cosα的值,把所求的式子利用兩角和的余弦函數公式化簡后,將每個三角函數值代入即可求出.
【考點精析】本題主要考查了兩角和與差的余弦公式和二倍角的正弦公式的相關知識點,需要掌握兩角和與差的余弦公式:![]() ;二倍角的正弦公式:
;二倍角的正弦公式:![]() 才能正確解答此題.
才能正確解答此題.


科目:高中數學 來源: 題型:
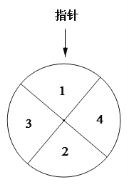
【題目】【2016高考山東文數】某兒童樂園在“六一”兒童節推出了一項趣味活動.參加活動的兒童需轉動如圖所示的轉盤兩次,每次轉動后,待轉盤停止轉動時,記錄指針所指區域中的數.設兩次記錄的數分別為x,y.獎勵規則如下:
①若![]() ,則獎勵玩具一個;
,則獎勵玩具一個;
②若![]() ,則獎勵水杯一個; ③其余情況獎勵飲料一瓶.
,則獎勵水杯一個; ③其余情況獎勵飲料一瓶.
假設轉盤質地均勻,四個區域劃分均勻.小亮準備參加此項活動.
(I)求小亮獲得玩具的概率;
(II)請比較小亮獲得水杯與獲得飲料的概率的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數, ![]() ).
).
(Ⅰ)把曲線![]() 的極坐標方程化為直角坐標方程,并說明曲線
的極坐標方程化為直角坐標方程,并說明曲線![]() 的形狀;
的形狀;
(Ⅱ)若直線![]() 經過點
經過點![]() ,求直線
,求直線![]() 被曲線
被曲線![]() 截得的線段
截得的線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
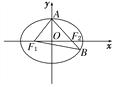
【題目】如圖,F1,F2分別是橢圓C:![]() 的左、右焦點,A是橢圓C的頂點,B是直線AF2與橢圓C的另一個交點,∠F1AF2=60°.
的左、右焦點,A是橢圓C的頂點,B是直線AF2與橢圓C的另一個交點,∠F1AF2=60°.
(1)求橢圓C的離心率;
(2)已知△AF1B的面積為40![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲、乙兩名學生中選拔一人參加射箭比賽,為此需要對他們的射箭水平進行測試.現這兩名學生在相同條件下各射箭10次,命中的環數如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)計算甲、乙兩人射箭命中環數的平均數和標準差;
(2)比較兩個人的成績,然后決定選擇哪名學生參加射箭比賽.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠家具車間造A、B型兩類桌子,每張桌子需木工和漆工兩道工序完成.已知木工做一張A、B型桌子分別需要1小時和2小時,漆工油漆一張A、B型桌子分別需要3小時和1小時;又知木工、漆工每天工作分別不得超過8小時和9小時,而工廠造一張A、B型桌子分別獲利潤2千元和3千元,試問工廠每天應生產A、B型桌子各多少張,才能獲得利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
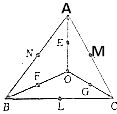
【題目】平面內有一個△ABC和一點O(如圖),線段OA,OB,OC的中點分別為E,F,G,BC,CA,AB的中點分別為L,M,N,設 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)試用 ![]() ,
, ![]() ,
, ![]() 表示向量
表示向量 ![]() ,
, ![]() ,
, ![]() ;
;
(2)證明:線段EL,FM,GN交于一點且互相平分.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com