
【題目】如果你留心使會發現,汽車前燈后的反射鏡呈拋物線的形狀,把拋物線沿它的對稱軸旋轉一周,就會形成一個拋物面.這種拋物面形狀,正是我們熟悉的汽車前燈的反射鏡形狀,這種形狀使車燈既能夠發出明亮的、照射很遠的平行光束,又能發出較暗的,照射近距離的光線.我們都知道常規的前照燈主要是由燈泡、反射鏡和透鏡三部分組成,明亮的光束,是由位于拋物面形狀反射鏡焦點的光源射出的,燈泡位于拋物面的焦點上,燈泡發出的光經拋物面反射鏡反射形成平行光束,再經過配光鏡的散射、偏轉作用,以達到照亮路面的效果,這樣的燈光我們通常稱為遠光燈:而較暗的光線,不是由反射鏡焦點的光源射出的,光線的行進與拋物線的對稱軸不平行,光線只能向上和向下照射,所以照射距離并不遠,如果把向上射出的光線遮住.車燈就只能發出向下的、射的很近的光線了.請用數學的語言歸納表達遠光燈的照明原理,并證明.
【答案】遠光燈照明原理:由拋物線的焦點所在的光源發出的光線經拋物線反射后與拋物線的對稱軸平行,證明見解析
【解析】
設![]() 為拋物線上一點,法線與
為拋物線上一點,法線與![]() 軸交于
軸交于![]() ,反射光線為
,反射光線為![]() ,
,![]() 為拋物線的焦點,
為拋物線的焦點,![]() 的斜率,根據角的正切值,證明
的斜率,根據角的正切值,證明![]() 即可.
即可.
遠光燈照明原理:由拋物線的焦點所在的光源發出的光線經拋物線反射后與拋物線的對稱軸平行.
證明:不妨設拋物線方程為:y2=2px(p>0),焦點為F,P為拋物線上一點,FP的反射光線為PN,
如圖所示:設拋物線過點P的切線為直線l,法線交x軸于M,
由光的反射性質可知∠FPM=∠MPN,
由y2=2px,不妨設P在第一象限,P(![]() ,y0),
,y0),
當y0=0時,直線l與y軸重合,顯然PN與x軸重合,
當y0≠0時,設直線l的斜率為k,
則直線l的方程為:y=k(x![]() )+y0,
)+y0,
代入拋物線方程可得:ky2﹣2py﹣ky02+2py0=0,
令△=4p2﹣4k(2py0﹣ky02)=0可得k![]() ,
,
故法線PM的斜率為![]() .
.
不妨設P在第一象限,設∠PMx=α,∠PFM=β,∠NPM=θ,
則tanα![]() ,tanβ
,tanβ ,
,
∴tanθ=tan∠FPM=tan(α﹣β) .
.
∴tanθ+tanα=0,故α+θ=π,
∴PN∥x軸.



 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四邊形ABED中,AB//DE,AB![]() BE,點C在AB上,且AB
BE,點C在AB上,且AB![]() CD,AC=BC=CD=2,現將△ACD沿CD折起,使點A到達點P的位置,且PE
CD,AC=BC=CD=2,現將△ACD沿CD折起,使點A到達點P的位置,且PE![]() .
.
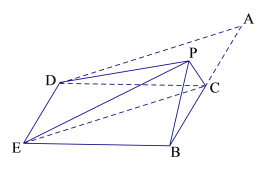
(1)求證:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱錐P-EBC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】人造地球衛星繞地球運行遵循開普勒行星運動定律:如圖,衛星在以地球的中心為焦點的橢圓軌道上繞地球運行時,其運行速度是變化的,速度的變化服從面積守恒規律,即衛星的向徑(衛星與地心的連線)在相同的時間內掃過的面積相等設該橢圓的長軸長、焦距分別為![]() ,
,![]() .某同學根據所學知識,得到下列結論:
.某同學根據所學知識,得到下列結論:

①衛星向徑的取值范圍是![]()
②衛星向徑的最小值與最大值的比值越大,橢圓軌道越扁
③衛星在左半橢圓弧的運行時間大于其在右半橢圓弧的運行時間
④衛星運行速度在近地點時最小,在遠地點時最大
其中正確的結論是( )
A.①②B.①③C.②④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】卵形線是常見曲線的一種,分笛卡爾卵形線和卡西尼卵形線,卡西尼卵形線是平面內與兩個定點(叫焦點)的距離之積等于常數的點的軌跡.某同學類比橢圓與雙曲線對卡西尼卵形線進行了相關性質的探究,設F1(﹣c,0),F2(c,0)是平面內的兩個定點,|PF1||PF2|=a2(a是常數).得出卡西尼卵形線的相關結論:①該曲線既是軸對稱圖形也是中心對稱圖形;②若a=c,則曲線過原點;③若0<a<c,其軌跡為線段.其中正確命題的序號是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,若函數
時,若函數![]() 的導函數
的導函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() ,
, ![]() 兩點,其橫坐標分別為
兩點,其橫坐標分別為![]() ,
, ![]() ,線段
,線段![]() 的中點的橫坐標為
的中點的橫坐標為![]() ,且
,且![]() ,
, ![]() 恰為函數
恰為函數![]() 的零點,求證:
的零點,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設不等式![]() 表示的平面區別為
表示的平面區別為![]() .區域
.區域![]() 內的動點
內的動點![]() 到直線
到直線![]() 和直線
和直線![]() 的距離之積為2.記點
的距離之積為2.記點![]() 的軌跡為曲線
的軌跡為曲線![]() .過點
.過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
(1)求曲線![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 軸,
軸,![]() 為曲線
為曲線![]() 上一點,求
上一點,求![]() 的取值范圍;
的取值范圍;
(3)若以線段![]() 為直徑的圓與
為直徑的圓與![]() 軸相切,求直線
軸相切,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為等差數列,前
為等差數列,前![]() 項和為
項和為![]() ,
,![]() 是首項為
是首項為![]() 的等比數列,且公比大于
的等比數列,且公比大于![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)設![]() ,
,![]() 為數列
為數列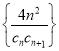 的前
的前![]() 項和,求不超過
項和,求不超過![]() 的最大整數.
的最大整數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱柱![]() 的側棱與底面垂直,
的側棱與底面垂直,![]() ,
,![]() ,M是
,M是![]() 的中點,
的中點,![]() 是
是![]() 的中點,點
的中點,點![]() 在
在![]() 上,且滿足
上,且滿足![]() .
.
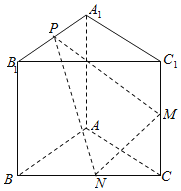
(1)證明:![]() .
.
(2)當![]() 取何值時,直線
取何值時,直線![]() 與平面
與平面![]() 所成的角
所成的角![]() 最大?并求該角最大值的正切值.
最大?并求該角最大值的正切值.
(3)若平面![]() 與平面
與平面![]() 所成的二面角為
所成的二面角為![]() ,試確定P點的位置.
,試確定P點的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點
的右焦點![]() 與拋物線
與拋物線![]() 的焦點重合,原點到過點
的焦點重合,原點到過點![]() ,
,![]() 的直線的距離是
的直線的距離是![]() .
.
![]() 1
1![]() 求橢圓
求橢圓![]() 的方程;
的方程;
![]() 2
2![]() 設動直線
設動直線![]() 與橢圓
與橢圓![]() 有且只有一個公共點
有且只有一個公共點![]() ,過
,過![]() 作
作![]() 的垂線與直線
的垂線與直線![]() 交于點
交于點![]() ,求證:點
,求證:點![]() 在定直線上,并求出定直線的方程.
在定直線上,并求出定直線的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com